
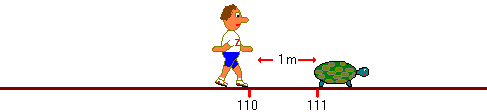
Paradoxul lui Zenon: Ahile şi broasca ţestoasă.
Nu știu niciun jurnalist de știință autentic în presa generalistă de la noi. Cei care scriu despre știință, de regulă traduc (ceea ce este meritoriu), dar nu înțeleg. C. T. Popescu este un caz aparte, în sensul că acesta se străduiește să înțeleagă când vorbește despre lucruri care țin de știință. La un moment dat, de exemplu, acesta scrie despre concepte complexe, precum „universul observabil”, „materia întunecată și energia întunecată” și vidul din interiorul atomului. Am scris un articol în care am explicat ce a înțeles corect și ce nu.
Recent „gazetarul” (cum vrea să fie numit, pentru a se delimita de jurnaliștii de tip nou, cu care nu vrea să fie asociat) spune că a rezolvat „paradoxul lui Zenon”. E o afirmație îndrăzneață, căci paradoxul a dat bătăi de cap multor mari gânditori de-a lungul timpului, așa că merită să urmărim firul gândirii acestuia.
Ce este paradoxul lui Zenon?
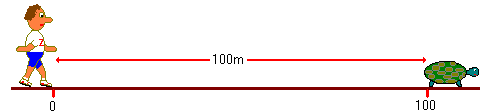
Paradoxul lui Zenon denumit „Ahile şi broasca ţestoasă" încearcă să demonstreze concluzia conform căreia cel care aleargă mai repede nu îl va întrece niciodată pe cel care aleargă mai încet.
Să ne imaginăm o întrecere între celebrul atlet Ahile și un rival mai lent, transformat de legendă într-o broască ţestoasă (la acea vreme broasca ţestoasă era simbolul înţelepciunii). Să presupunem că Ahile are o viteză de două ori mai mare decât cea a ţestoasei. Ţestoasa are un avans de 1 km faţă de Ahile (acesta plecând din origine). Oricine va trage concluzia că peste 2 km Ahile va ajunge ţestoasa.
Dar Zenon ne spune altceva: când Ahile ajunge la 1 km, ţestoasa a ajuns la 1 km şi jumătate, iar când Ahile ajunge la 1 km şi jumătate, broasca a ajuns la 1 km şi trei sferturi şi aşa mai departe, astfel că niciodată Ahile nu va reuşi să întreacă broasca ţestoasă.
Cum rezolvă gazetarul paradoxul?
Articolul integral îl puteți citi integral aici. Dar paragrafele care contează (în care „rezolvă” paradoxul) sunt următoarele:
„Soluția stă în definirea termenului „distanță”. Avem fenomenul observabil că Ahile o rupe la fugă, depășește broasca și câștigă cursa.
Zenon zice însă că Ahile trebuie să parcurgă mai întâi distanța până unde era broasca. În natură, nu există distanțe. Ca să vorbim de distanță, trebuie să vorbim de măsură; distanța, ca să existe, trebuie măsurată – din ochi, cu rigla, sau cu satelitul.
Astfel, Zenon mută discuția din planul real, în planul conceptual, procesul de măsurare petrecându-se în psihicul uman, fără corespondent în natură.
Există în natură 1 metru? Nu. Există în natură o jumătate? Asta înseamnă două părți egale. Există în natură două cevauri egale? Nicidecum. Oricât de precis am despica un măr cu laserul, să zicem, cele două „jumătăți” nu vor fi „egale” decât până la precizia de măsurare. Dincolo de ea, nu mai știm.
Măsurarea, operațiune umană, este întotdeauna aproximativă. Ea suportă divizarea la infinit.
Să zicem că luăm o unitate de măsură foarte mică pentru a măsura distanța Ahile-locul unde era broasca. Întotdeauna va exista o unitate de măsură și mai mică, dar diferită de 0, pentru că atunci nu mai măsurăm nimic, care aproximează și mai bine punctul respectiv.
Zenon transferă faptul adevărat al aproximației infinite în procesul măsurării, din plan abstract psihic în planul real, unde el e fals, pentru că în realitate lucrurile sunt, nu se măsoară”. (sublinierile ne aparțin)
Ce spune CTP, în esență? Că „distanța” nu există în natură, iar activitatea de măsurare, o activitate prin excelență umană (e doar în mintea omului), este imprecisă, orice am face. Iar măsurarea suportă divizarea la infinit. Măsurarea nu are legătură cu realitatea, unde „lucrurile sunt, nu se măsoară”. Așadar, într-o propoziție, pentru că măsurătoarea nu poate arăta cât anume este o distanță cu precizie infinită, distanța nu există. Și cu asta basta! Nu mai avem niciun paradox!
Sincer, demonstrația mi se pare cam cum a demonstrat Gödel că Dumnezeu există :) Nu că ar fi demonstrațiile asemănătoare în abordare, ci că demonstrația de față, ca și cea a lui Gödel, este cam... trasă de păr.
Unde e problema cu paradoxul lui Zenon?
Problema este că spațiul nu există ca un sistem de coordonate pe caietul de matematică. Spațiul, din ce știm, nu are componente structurale fundamentale, nu are celule de spațiu, care sunt indivizibile și care puse împreună formează totalitatea spațiului. Nu există cea mai mică unitate de spațiu. Ba mai mult, relativitatea generală ne spune că spațiul este dinamic, distorsionat de materia și energia din univers (fenomenul gravitației, nu prea bine înțeles, la nivel fundamental).
Spațiul nu pare a fi, așadar, discret. Iar dacă nu este discret, atunci este continuu. O complicație fatală (pe care a intuit-o Zenon) este că dacă poți împărți spațiul la infinit, atunci mișcarea nu este posibilă. Ca să te deplasezi de la punctul A la punctul B trebuie să treci printr-o infinitate de puncte intermediare, ceea ce nu este logic posibil (chiar dacă este clar că în realitate este posibil).
Paradoxul lui Zenon este însă nerezolvabil
Există unele soluții matematice. Puteți citi un mai vechi articol al nostru pe acest subiect aici.
Paradoxul este rezolvat dacă 0,(9) = 1
Să spunem că vrei să te deplasezi de acasă până la magazinul din colț. Întâi, evident, trebuie să treci prin punctul care marchează jumătatea distanței dintre locul în care te afli și cel de destinație. Dar înainte de asta trebuie să treci prin punctul care marchează mijlocul distanței dintre locul în care te afli și punctul care marchează mijlocul distanței dintre tine și magazin șamd.
Matematic, povestea se scrie așa: 1/2 (jumătatea distanței) + 1/4 (sfertul distanței) + 1/8 + 1/16 + 1/32 + ... . O serie infinită.
Dacă aduni primii 10 termeni ai seriei obții 0,999, iar dacă aduni primii 20 de termeni obții 0,999999. Pe măsură ce aduni mai mulți termeni, te apropii tot mai mult de 1, dar nu ajungi niciodată la 1.
Dacă ai obține 1, atunci ai rezolva paradoxul lui Zenon, pentru că 1 reprezintă distanța dintre tine și magazin.
Ok, și atunci? Atunci unii matematicieni spun că, deși contraintuitiv, 0,(9) = 1. Dacă accepți asta, ca mulți matematicieni, totul e ok. Dacă nu accepți, rămânem cu problema nerezolvată.
Matematicienii justifică și prin următorul calcul simplu că 0,(9) = 1:
0,33333... = 1/3, iar dacă înmulțim ambii termeni cu 3 vom obține
0,99999... = 3/3 = 1.
Sigur, oricum am face, trebuie să credem că 0,(9) = 1. Sau nu.
Ca să fie clar, discuțiile dacă este acceptabil să spunem că 0,(9) = 1 au loc și între matematicieni, nu doar între profani.
De ce e nerezolvabil paradoxul
Dar conceptual paradoxul este nerezolvabil. Pentru simplu motiv că suntem obligați să lucrăm cu un concept care reprezintă, în fapt, o limită de nedepășit a minții umane: conceptul de infinit. Puteți citi un un articol în care prezentăm limitele minții umane aici.
Conceptul de infinit este neștiințific (în afara științei) și nu poate fi utilizat pentru a rezolva problemele științei. În plus, nu avem cum lămuri problema mișcării dintr-un punct în altul, atâta vreme cât nu știm dacă există puncte intermediare, adică dacă nu știm aproape nimic despre natura spațiului. Nu voi insista pe acest subiect aici. Puteți citi articolul nostru „Spațiul nu are o existență în sine”.
În esență, dificultatea paradoxului constă în faptul că ne lovim de limite biologice ale minții umane. Faptul că nu înțelegem infinitul ne împiedică să găsim o rezolvare, deși, din nou, știm că deplasarea are loc în natură, căci am fost martorii unui tren care pleacă de la Constanța și ajunge (chiar și cu mari întârzieri) la București.
Toate eforturile în a rezolva „paradoxul lui Zenon” au fost zadarnice pentru un motiv simplu, dar descurajant: nu avem instrumentele pentru a-l rezolva; pur și simplu sunt subiecte pentru care nu suntem înzestrați mental, oricâtă ingeniozitate am folosi. Infinitul este o limită fundamentală și definitivă a înțelegerii noastre, iar infinitul este conceptul-cheie în „paradoxul lui Zenon”.
Și ce a rezolvat CTP, până la urmă?
În opinia mea, nimic. Dar raționamentul acestuia pare, sub un anumit aspect, că se apropie de opinia exprimată mai sus. CTP pare că spune că infinitul apare doar în gândirea umană, dar el nu se regăsește în natură: „Zenon transferă faptul adevărat al aproximației infinite în procesul măsurării, din plan abstract psihic în planul real, unde el e fals, pentru că în realitate lucrurile sunt, nu se măsoară”.
Dar infinitul nu există nici în natură, nici în mintea umană, ci este doar un concept uman ce indică neputința noastră, o limită a minții umane. Că facem această delimitare: măsurătoarea este în mintea noastră, distanța nu există în natură - nu cred că rezolvă în niciun fel problema, adică paradoxul lui Zenon.
Limitele minții umane lasă anumite subiecte de interes pentru noi oamenii de nerezolvat. Paradoxul lui Zenon este unul dintre acestea.
P.S. Ca să nu se creadă că aceasta este o critică de dragul criticii, voi spune sincer că apreciez aceste încercări ale lui C. T. Popescu de a gândi probleme dificile, chiar dacă, în opinia mea, nu are timpul necesar pentru a înțelege complexitatea subiectelor pe care le „atacă”. Dar este meritoriu că vorbește despre subiecte majore, complicate și nerezolvate din știință. Face, prin urmare, un serviciu științei.
Pe de altă parte, mie nu mi-e clar unde sunt miile de minți luminate ale acestei țări, care cer permanent fonduri pentru cercetare, dar care nu găsesc timp să scrie un articol de știință într-un limbaj accesibil publicului larg. E de mirare că la noi cercetătorii trăiesc exclusiv în jargonul de nepătruns al domeniului lor științific, iar publicarea unor articole inteligibile despre munca lor nu pare a fi în interesul lor. E de mirare că despre subiecte complicate din știință vorbesc la televizor blogări de ocazie (cu o înțelegere aproximativă a subiectelor despre care vorbesc) sau, din nou, CTP...
