Revenim cu o nouă pastilă de matematică transpusă în versuri. De data aceasta vă prezentăm o scurtă problemă de perspicacitate, în care autorul vă invită să stabiliţi modul în care călătorii urcă în vagoanele unui tren. Soluţia o vom oferi în scurtă vreme.
- Detalii
- de: Petre Rău
- Matematica
Revenim cu o nouă pastilă de matematică transpusă în versuri. De data aceasta vă prezentăm o scurtă problemă de logică, în care autorul vă invită să stabiliţi ce număr urmează într-un şir constituit după o anumită logică. Soluţia o vom oferi în scurtă vreme.
- Detalii
- de: Petre Rău
- Matematica
Ne întoarcem cu matematica transpusă în versuri. De data aceasta vă prezentăm două scurte probleme cu beţe de chibrit, în care autorul vă invită să rezolvaţi două calcule aparent simple, mutând un singur băţ. Ca de obicei, vă oferim şi soluţia în josul paginii.
- Detalii
- de: Petre Rău
- Matematica
O nouă problemă-poezie. De data aceasta vă prezentăm o problemă interesantă având ca subiect firele de păr de pe capul... gălăţenilor. Dacă sunteţi din Galaţi, trebuie musai să vedeţi despre ce e vorba. Dacă nu, curiozitatea nu vă va lăsa pasivi.
- Detalii
- de: Petre Rău
- Matematica
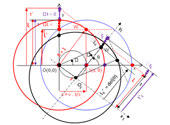Supermatematica s-a născut din efortul milenar şi disperat al omului de-a modela lumea aşa cum este ea: complexă şi neliniară, nu liniară şi simplistă. Supermatematica este împlinirea visul matematicienilor de-a avea o infinitate de matematici şi de-a opera cât mai simplu cu ele.
- Detalii
- de: Mircea Eugen Selariu
- Matematica
O nouă problemă-poezie, de data aceasta despre un melc rătăcit într-o fântână, care doreşte - habar nu avem de ce :) - să ajungă la lumină. Ca de obicei, puteţi să vă stoarceţi creierii în tihnă pentru a rezolva problema, dar dacă nu merge, aveţi răspunsul în partea de jos.
- Detalii
- de: Petre Rău
- Matematica
Iată o metodă interesantă de a face matematica atractivă şi distractivă, prin intermediul poeziei. Începând de astăzi vă vom oferi regulat o serie de poezii scrise de matematicianul şi scriitorul Petre Rău. Prima poezie este despre paradoxul lui Zenon.
- Detalii
- de: Petre Rău
- Matematica
Multe din problemele de comutativitate în grupuri, altfel delicate, se rezolvă mai uşor dacă ţinem seama de structura algebrică de subgrup a centrului unui grup.
Manevrele posibile ale unui cub Rubik formează un grup
Credit imagine: Wikimedia Commons
Definiţie: Fie {tex}(G,\cdot ){/tex} un grup şi {tex}X\subset G{/tex} o submulţime a sa. Mulţimea {tex}Z(X)=\{g\in G|gx=xg,\forall x\in X\}{/tex} se numeşte centralizatorul mulţimii X.
Definiţie: Mulţimea {tex}Z(G)=\{g\in G|gx=xg,\forall x\in G\}{/tex} se numeşte centrul grupului G.
Propoziţie: Pentru orice mulţime {tex}X\subset G,(Z(X),\cdot ){/tex} este subgrup al grupului {tex}(g,\cdot ){/tex}.
Dacă {tex}g_1,g_2\in Z(X){/tex} avem {tex}(g_1g_2)x=g_1(g_2x)=g_1(xg_2)=(g_1x)g_2=x(g_1g_2){/tex} deci {tex}g_1g_2\in Z(X){/tex}.
Din {tex}g_1x=xg_1{/tex} rezultă {tex}xg_1^{-1}=g_1^{-1}x{/tex} deci {tex}g_1^{-1}\in Z(X){/tex}.
Observaţie: Subgrupul {tex}Z(X){/tex} este format din elementele lui G care comută cu toate elementele mulţimii X.
Definiţie: Mulţimea {tex}N(X)=\{g\in G|gX=Xg\}{/tex} se numeşte normalizatorul mulţimii X.
Propoziţie: Pentru orice submulţime {tex}X\subset G{/tex}, normalizatorul {tex}(N(X),\cdot ){/tex} este subgrup al grupului {tex}(G,\cdot ){/tex}. (Demonstraţia se face analog cu cea de la centrul grupului)
Consecinţe:
1. {tex}Z(X){/tex} este subgrup al lui {tex}N(X){/tex}
2. Dacă H este subgrup al lui G, atunci H este subgrup al lui N(H).
3. Fie {tex}(G,\cdot ){/tex} un grup şi {tex}n,p\in Z{/tex}. Notăm cu {tex}(n,p)=1{/tex}. Dacă {tex}\forall x\in G{/tex} şi {tex}x^n\in Z(G){/tex} şi {tex}x^p\in Z(G){/tex}, atunci {tex}(G,\cdot ){/tex} este grup abelian.
Bibliografie: G.M. 4-5/1990.
- Detalii
- de: Adrian Olteanu
- Matematica
În cele ce urmează vă prezentăm formulele mediilor aritmetică, geometrică, pătratică şi armonică a n numere.
Formula mediei aritmetice a n numere
{tex}\dfrac{a_1+a_2+...+a_n}{n}{/tex}
Formula mediei geometrice a n numere
{tex}\displaystyle \sqrt[n]{a_1\cdot a_2\cdot a_3 \cdot ... \cdot a_n}{/tex}
Formula mediei pătratice a n numere
{tex}\sqrt {\dfrac {{a_1}^2 + {a_2}^2 + .. + {a_n}^2}{n}}{/tex}
Formula mediei armonice a n numere
{tex}\dfrac{n}{\frac{1}{a_1} + \frac {1}{a_2} + ... + \frac{1}{a_n}}{/tex}
- Detalii
- de: Adrian Buzatu
- Matematica
În articolul următor vă prezentăm formulele ariei, lungimii şi, după caz, volumului unor figuri geometrice uzuale: cerc, con, cilindru şi sferă.
Aria cercului de rază R:
{tex}A = \pi R^2{/tex}
Lungimea cercului de rază R:
{tex}L = 2 \pi R{/tex}
Aria laterală a conului de rază r şi înălţime h:
{tex}S=\pi r\sqrt{r^2+h^2}{/tex}
Aria bazei conului de rază r şi înălţime h:
{tex}S=\pi r^2{/tex}
Volumul conului de rază r şi înălţime h:
{tex}V=\frac{\pi r^2\cdot h}{3}{/tex}
Aria cilindrului de rază r şi înălţime h (cele două baze + laterală):
{tex}S=2\pi r^2 + 2\pi r \cdot h{/tex}
Volumul cilindrului de rază r şi înălţime h:
{tex}V=2\pi r^2}\cdot h{/tex}
Aria sferei de rază r:
{tex}S=4\pi r^2{/tex}
Volumul sferei de rază r:
{tex}V=\frac{4\pi r^3}{3}{/tex}
- Detalii
- de: Adrian Buzatu
- Matematica
Pornind de la un articol anterior - Introducere în inducția matematică - vom enumera în continuare câteva aplicaţii ale inducţiei matematice, cât şi modul lor de demonstrare. Astfel, veţi putea realiza felul în care metoda trebuie aplicată, cât şi genul de probleme la care se aplică.
credit: http://math.njit.edu
Suport teoretic pentru principiul inducţiei matematice
Pentru a vă revizui cunoştinţele teoretice legate de inducția matematică, vă sugerăm să citiţi: Introducere în inducția matematică.
Exercițiul 1
Un exemplu simplu ar fi problema următoare:
Demonstraţi că: {tex}P(n) : 1+2+3+...+n= \frac{n \cdot (n+1)}{2}{/tex} pentru orice n - număr natural nenul.
Vom rezolva acestă problemă fără a apela la principiul lui Gauss.
Rezolvarea este prezentată în continuare:
Vom demonstra problema dată folosind metoda inducţiei matematice. Astfel, vom verifica cele 2 etape:
- etapa de verificare: luăm n-minim, adică {tex}n=1{/tex}.
Avem {tex}P(1) : 1= \frac{1 \cdot 2}{2}{/tex} - propoziţie adevărată. Deci etapa de verificare a fost realizată.
- etapa de demonstraţie: trebuie să demonstrăm că dacă {tex}P(n){/tex} este adevărată, atunci {tex}P(n+1){/tex} este adevărată.
Avem:
{tex}1+2+3+...+n+(n+1) = (1+2+3+...+n)+(n+1)=\frac{n \cdot (n+1)}{2} + (n+1) =\frac{n \cdot (n+1) + 2 \cdot (n+1)}{2} =\frac{(n+2) \cdot (n+1)}{2}{/tex}
Astfel avem demonstrată propoziţia {tex}P(n+1){/tex}.
Deci și etapa de demonstrație a fost finalizată.
Folosind metoda inducţiei matematice am demonstrat că: {tex}P(n) : 1+2+3+...+n= \frac{n \cdot (n+1)}{2}{/tex} pentru orice n - număr natural nenul.
Exercițiul 2
De asemenea, mai putem da ca și exemplu problema următoare:
Să se demonstreze că pentru orice {tex}n \geq 1{/tex}, n - număr natural, avem:
{tex}1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{2n-1} - \frac{1}{2n} = \frac{1}{n+1} + \frac{1}{n+2} + ... + \frac{1}{2n}{/tex}.
Demonstrație:
Notăm cu {tex}P(n){/tex} egalitatea de mai sus, pentru numărul n.
Vom demonstra problema folosind metoda inducției matematice. Deci, vom verifica cele două etape:
- etapa de verificare:
Alegem n-minim, adică {tex}n=1{/tex}. Astfel, egalitatea dată devine {tex}1 - \frac{1}{2} = \frac{1}{2}{/tex}. Deci {tex}P(1){/tex} este adevărată. Astfel, etapa de verificare este demonstrată.
- etapa de demonstrație:
Demonstrăm că dacă {tex}P(k){/tex} este adevărată, atunci {tex}P(k+1){/tex} este adevărată.
{tex}P(k): 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{2k-1} - \frac{1}{2k} = \frac{1}{k+1} + \frac{1}{k+2} + ... + \frac{1}{2k}{/tex}
{tex}P(k+1): 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{2k-1} - \frac{1}{2k} + \frac{1}{2k+1} - \frac{1}{2(k+1)} = \frac{1}{k+2} + \frac{1}{k+3} + ... + \frac{1}{2(k+1)}{/tex}
Scăzând membru cu membru egalităţile de mai sus (prima egalitate dintr-a doua ), obţinem egalitatea:
{tex}\frac{1}{2k+1} - \frac{1}{2(k+1)} = \frac{1}{2k+1} + \frac{1}{2k+2} - \frac{1}{k+1}{/tex}
Dar aceasta este evident adevărată.
Astfel, cum {tex}P(k){/tex} este adevărată şi propoziţia de mai sus este şi aceasta adevărată, atunci şi {tex}P(k+1){/tex} este adevărată.
Aşadar, etapa de demonstraţie a fost realizată.
Conform metodei inducţiei matematice avem:
{tex}1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{2n-1} - \frac{1}{2n} = \frac{1}{n+1} + \frac{1}{n+2} + ... + \frac{1}{2n}{/tex} pentru orice {tex}n \geq 1{/tex}, n - număr natural.
Exercițiul 3
Majoritatea problemelor care se rezolvă prin metoda inducţiei matematice nu ne indică formula generală ce trebuie demonstrată. În acele cazuri, trebuie sa verificăm ceea ce ni se dă pentru câteva valori particulare, iar apoi să observăm formula generală. O astfel de problemă este următoarea:
Să se calculeze suma: {tex}\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + ... + \frac{1}{n \cdot (n+1)}{/tex} pentru orice n - număr natural {tex}n \geq 1{/tex}.
Demonstraţie:
Notăm suma de mai sus cu {tex}S(n){/tex}. Ca să obţinem expresia generală, vom verifica mai întâi câteva cazuri particulare, adică {tex}n=1, n=2, n=3{/tex} şi obţinem:
{tex}S(1) = \frac{1}{1 \cdot 2} = \frac{1}{2}{/tex}
{tex}S(2) = \frac{1}{2} + \frac{1}{2 \cdot 3} = \frac{1}{2} + \frac {1}{6} = \frac {4}{6} = \frac {2}{3}{/tex}
{tex}S(3) = \frac{1}{2} + \frac{1}{2 \cdot 3} +\frac{1}{3 \cdot 4} = \frac{1}{2} + \frac {1}{6} + \frac{1}{12} = \frac{6+2+1}{12} = \frac{9}{12} = \frac{3}{4}{/tex}
Observând sumele de mai sus constatăm că {tex}S(n) = \frac{n}{n+1}{/tex}.
Astfel că am ajuns la etapa în care am intuit o expresie generală, şi vom încerca să o demonstrăm prin metoda inducţiei matematice.
Lăsăm restul rezolvării problemei ca şi exerciţiu în care să aplicaţi raţionamentul inducţiei matematice.
Articol scris pe baza unor manuale de matematică de clasa a IX-a.
- Detalii
- de: Tiberiu Puican
- Matematica
Inducţia matematică reprezintă un procedeu ce poate fi folosit în cadrul rezolvării unor probleme de algebră. Prin aceasta se înţelege o metodă de raţionament care conduce de la propoziţii particulare la o oarecare propoziţie generală. Aşa cum este prezentată în majoritatea manualelor şcolare, se lasă o falsă impresie cum că aceasta ar fi folosită numai pentru demonstrarea unor formule date. Însă inducţia poate fi folosită pentru rezolvarea unor probleme cu rezultat mult mai complex, a căror soluţionare ar fi mult mai grea dacă nu am utiliza această metodă.
credit: http://math.njit.edu
Principiul inducţiei matematice
Principiul pe care se bazează inducţia matematică este:
Fie {tex}P(n){/tex} o propoziţie care depinde de un număr natural {tex}n \geq m{/tex}, m fiind un număr natural fixat. Demonstraţia prin metoda inducţiei matematice a propoziţiei {tex}P(n){/tex}, constă din două etape:
1. Se verifică mai întâi că {tex}P(m){/tex} este adevărată.
2. Se presupune că {tex}P(k){/tex} este adevărată şi se demonstrează că {tex}P(k+1){/tex} este adevărată, k fiind un număr natural mai mare sau egal cu m (adică {tex}P(k) \Rightarrow P(k+1){/tex} , {tex}k \geq m{/tex} ).
Dacă ambele etape ale demonstraţiei sunt verificate, atunci propoziţia {tex}P(n){/tex} este adevărată pentru orice număr natural {tex}n \geq m{/tex} .
Intuitiv, această metodă de demonstraţie se justifică astfel:
Din {tex}P(m){/tex} adevărată şi {tex}P(k) \Rightarrow P(k+1){/tex}, pentru orice {tex}k \geq m{/tex}, rezultă că {tex}P(m+1){/tex} este adevărată (unde {tex}k=m{/tex} ); apoi, luând {tex}k=m+1{/tex} se obţine că {tex}$ P(m+2) ${/tex} este adevărată, şi aşa mai departe. Raţionând "din aproape în aproape" deducem că propoziţia {tex}P(n){/tex} este adevărată pentru orice număr natural {tex}n \geq m{/tex} .
Metoda inducţiei matematice ne arată că dacă {tex}P(1){/tex} este adevărată (pentru {tex}m=1{/tex}), şi din {tex}P(k) \Rightarrow P(k+1){/tex}, pentru {tex}k \geq 1{/tex}, unde k este număr natural, avem că {tex}P(k){/tex} este adevărat pentru orice k număr natural.
Câteva aplicaţii rezolvate puteţi găsi în cadrul articolului: Inducţia matematică - Aplicaţii.
Articol scris pe baza unor manuale de matematică de clasa a IX-a.
- Detalii
- de: Tiberiu Puican
- Matematica
În acest articol vă prezentăm o scurtă lecţie de algebră despre grupul lui Klein.
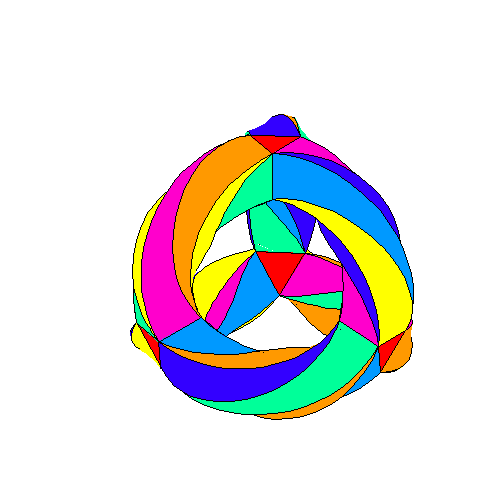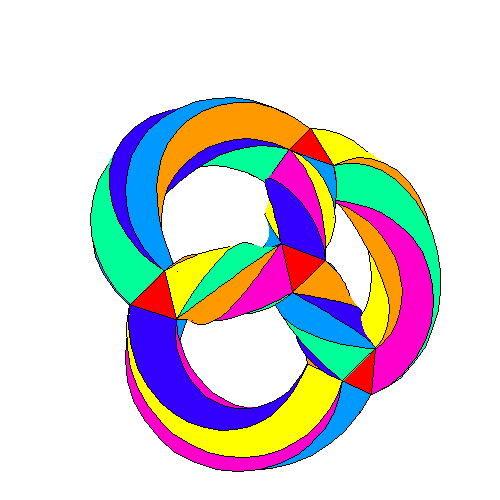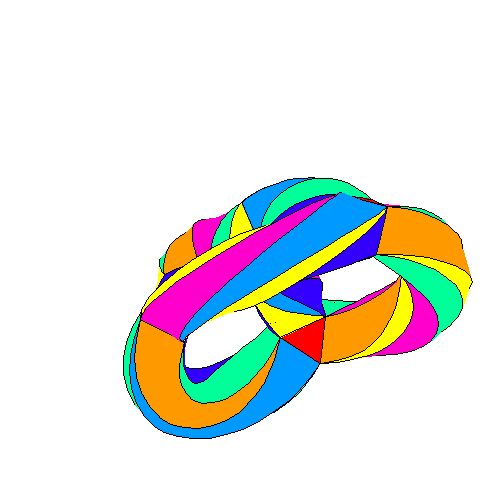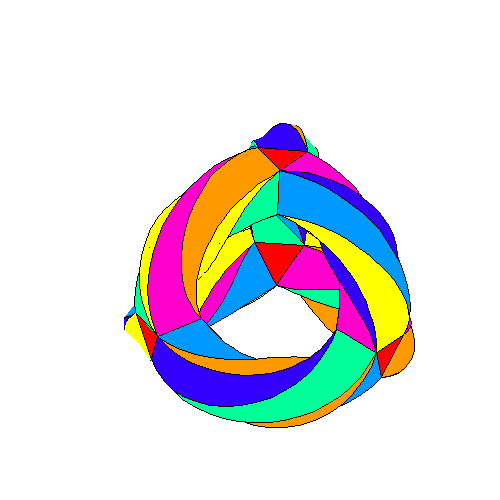
Curba cuartică a lui Klein
credit: Greg Egan
Fie mulţimea {tex}K = \{ e, a, b, c \}{/tex} înzestrată cu o lege de compoziţie definită prin următorul tabel:
Observaţi că pe diagonala principală a tabelului avem elementul „E”, care este şi elementul neutru al legii de compoziţie, iar pe diagonala secundară avem elementul „C”, care reprezintă compunerea dintre „A” şi „B”. Aşadar oricare ar fi elementul {tex}x \in K{/tex} , el are proprietatea că {tex}x^2 = e{/tex} .
Acesta este grupul lui Klein, un grup finit, comutativ, cu patru elemente, deci ordinul: {tex}ordK = 4{/tex}. Vă rămâne vouă ca exerciţiu să demonstraţi prin calcul această afirmaţie. Acest tip de grup a fost creat de matematicianul german Felix Klein în 1884 pentru a studia simetriile bidimensionale şi tridimensionale.
Sticla lui Klein, descrisă pentru prima dată în 1882 de către Felix Klein.
Un alt rezultat deosebit de interesant, pe care merită să îl demonstraţi, tot ca exerciţiu de algebră, este următorul: "Orice grup de 4 elemente este izomorf fie cu grupul lui Klein, fie cu grupul {tex}(\mathbb{Z}_4 , +){/tex}". Aşadar orice grup finit cu patru elemente îşi poate găsi o corespondenţă într-o simetrie geometrică.
- Detalii
- de: Mihai Bărbulescu
- Matematica
În nenumărate probleme de matematică sunt întâlnite conceptele de parte întreagă şi parte fracţionară a unui număr real. În articolul de mai jos definim aceste două concepte şi enumerăm principalele proprietăţi menite să vă ajute în rezolvarea problemelor de matematică cu parte întreagă şi parte fracţionară.
Fie {tex} $x\in\mathbb{R}${/tex} un număr real dat.
Definiţia 1: Se numeşte parte întreagă a numărului real {tex}x{/tex} cel mai mare număr întreg {tex}k{/tex} ce nu-l depăşeşte pe {tex}x{/tex}. Alternativ putem defini partea întreagă a lui {tex}x{/tex} având în vedere următoarele aspecte: pentru numărul real{tex}x{/tex} există şi este unic {tex}k\in\mathbb{Z}{/tex} cu proprietatea {tex}k\le x {/tex}.
Notaţie: Partea întreagă a lui {tex}x{/tex} se notează cu {tex}[x]{/tex}.
Definiţia 2: Se numeşte parte fracţionară a numărului real {tex}x{/tex} diferenţa dintre {tex}x{/tex} şi partea lui întreagă.
Notaţie: Partea fracţionară a lui {tex}x{/tex} se notează cu {tex}\{x\}{/tex}. Având în vedere această notaţie, partea fracţionară se defineşte astfel: {tex}\{x\}=x-[x]{/tex}.
Proprietăţi:
1) Pentru {tex}\forall k\in\mathbb{Z},[k]=k{/tex};
2) Pentru {tex}\forall k\in\mathbb{Z},\forall x\in\mathbb{R}{/tex} are loc egalitatea {tex}[x+k]=[x]+k{/tex};
3) Pentru {tex}\forall k\in\mathbb{Z},\forall x\in\mathbb{R}{/tex} are loc relaţia {tex}\{x+k\}=\{x\}{/tex};
4) Pentru {tex}\forall k\in\mathbb{Z}{/tex} avem {tex}\{k\}=0{/tex};
5) Pentru {tex}\forall x\in\mathbb{R}{/tex} avem {tex}0\le\{x\}<1{/tex};
6) Pentru {tex}\forall x,y\in\mathbb{R}{/tex} are loc {tex}[x+y]\ge[x]+[y]{/tex};
7) Pentru orice două numere reale pozitive {tex}x,y{/tex} are loc inegalitatea {tex}[xy]\ge[x][y]{/tex};
8) Pentru {tex}\forall n\in\mathbb{N^{*}},\forall x\in\mathbb{R}{/tex} este adevărată identitatea {tex}[\frac{x}{n}]=[\frac{[x]}{n}]{/tex};
9) Pentru {tex}\forall n\in\mathbb{N^{*}}, \forall x\in\mathbb{R}{/tex} are loc identitatea lui Hermite:
{tex}[x] + [x+\frac{1}{n}] + [x+\frac{2}{n}] +...+ [x+\frac{n-1}{n}]=[nx]{/tex}
sau în scriere prescurtată:
{tex}\dsiplaystyle \sum_{k=0}^{n-1} [x+\frac{k}{n}]=[nx]{/tex}
- Detalii
- de: Laurenţiu Tuca
- Matematica
Lecţie de algebră: inegalităţile mediilor aritmetică, geometrică, pătratică şi armonică.
Inegalităţile mediilor
{tex}\small \frac{n}{\frac{1}{a_1} + \frac {1}{a_2} + ... + \frac{1}{a_n}} \le \sqrt[n]{a_1\cdot a_2\cdot a_3 \cdot ... \cdot a_n} \le \frac{a_1+a_2+...+a_n}{n} \le \sqrt {\frac {{a_1}^2 + {a_2}^2 + .. + {a_n}^2}{n}}{/tex}
În figura de mai sus avem, în ordine, media armonică, media geometrică, media aritmetică şi media pătratică a n numere reale strict mai mari decât zero.
Dacă exemplificăm pe două numere a şi b, unde a este mai mic decât b, aceste inegalităţi arată astfel:
{tex}a \le \frac{2}{\frac{1}{a} + \frac {1}{b}} \le \sqrt{ab} \le \frac{a+b}{2} \le \sqrt {\frac {a^2 + b^2}{2}} \le b{/tex}
Egalitatea apare atunci când a=b.
- Detalii
- de: Iosif A.
- Matematica
