
În anul 1990 autorităţile au închis strada 42 din New York pentru parada dedicată zilei pământului, iar în anul 1999 un culoar important de trafic a fost închis în capitala Coreei de Sub pentru lucrări de reparaţii. În mod bizar, deşi ambele rute erau culoare importante de trafic, închiderea lor nu a dus la blocaje de circulaţie, ci la descongestionarea traficului.
Inspirate de această experienţă, autoritățile din Seul au demolat o autostradă care trecea prin centrul oraşului, şi nu numai că au descongestionat traficul, dar au şi putut crea un parc lung de aproximativ 7 km care a luat locul autostrăzii.
Reducerea timpului de parcurgere al unui traseu în urma eliminării unor străzi este un efect cu totul neprevăzut. Acest paradox a fost descoperit în anul 1968 de către profesorul Braess. El a descoperit ceea ce numim azi Paradoxul lui Braess: adăugarea unei muchii într-o reţea de transport poate creşte timpul de parcurgere a nodurilor din acea reţea.
Alte situaţii în care apare paradoxul lui Braess:
• într-un joc de baschet din 1999, eliminarea celui mai bun jucător dintr-o echipă a dus la câştigarea meciului de către acea echipă.
• a fost demonstrat matematic că reducerea ofertelor unui magazin poate creşte satisfacţia clienţilor. Având la dispoziţie o gamă prea largă de produse, cumpărătorii fac cu greu alegerea potrivită pentru nevoile personale, excluzând de multe ori varianta optimă. Reducând gama de produse existente într-un magazin, un comerciant poate îmbunătăţi satisfacţia clienţilor*
• în ecologie, extincţia unei specii pe cale de dispariţie poate creşte diversitatea într-o comunitate, prin evitarea extincţiilor secundare*
În reţeaua din figura de mai jos, timpul de parcurgere al unei străzi (laturi) depinde de „aglomeraţia” de pe acea stradă (în figură, numărul de indivizi care parcurg acea stradă la un moment dat este notat cu x). Deci, timpul de parcurgere al drumului de la A la D este 6x+26, indiferent de traseul ales: A-B-D sau A-C-D. Astfel, un grup de şase oameni care ar dori să se deplaseze de la A la D s-ar împărţi în două subgrupuri de câte trei şi astfel timpul de parcurgere al traseului ar fi de 6×3+26 = 44 de minute pentru fiecare individ.

Dacă adăugăm o autostradă de mare viteză, cu cost asociat fix, care uneşte locaţiile B şi C, ca în figura de mai jos, vor exista 4 rute posibile prin care oamenii vor putea parcurge traseul de la A la D: A-B-D, A-B-C-D, A-C-D şi A-C-B-D.
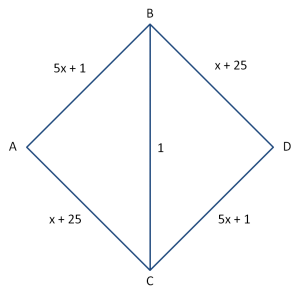
Pentru primul călător, cea mai rapidă rută va fi A-B-C-D, parcursă în 13 minute. Al doilea călător va alege aceeaşi rută, dar o va parcurge în 23 de minute. Al treilea şi al patrulea vor alege aceeaşi rută şi vor avea costurile 33 respectiv 43 de minute. Indivizii cinci şi șase pot parcurge oricare dintre rutele A-B-D sau A-C-D în 52 de minute. Deci, deşi adăugarea unei noi rute îmbunătăţeşte timpul de parcurgere al traseului A-D pentru primii călători, per ansamblu creste timpul de parcurgere cu aproape 20%.
Preluare de pe BlogulDespreStiinta, cu acordul editorului
