Cum să măsori fără... să măsori? Sună absurd, știu... Experiența de zi cu zi ne spune că singurul mod de a afla informații despre un obiect este de a-l analiza cu propriile simțuri sau prin diferite aparate menite să ne extindă simțurile (nu voi intra în detalii despre cât de real este de fapt ceea ce ne spun simțurile, deși puteți citi despre asta aici).
Mai mult, mecanica cuantică pare să ne spună că până la o măsurătoare directă nimic nu este bine definit în lume, totul fiind determinat de probabilități (de exemplu, o particulă elementară se află în „superpoziție”, până în momentul măsurării, care coincide cu colapsarea funcției de undă și identificarea unei poziții pentru particula măsurată).
Cu toate acestea, în acest articol încerc să arăt cum este posibil, cu ajutorul mecanicii cuantice, să obținem informații certe despre un obiect fără a interacționa cu el. Iar pentru a face totul mai interesant, haideți să lucrăm cu... bombe.
Să ne imaginăm că am dezvoltat un nou tip de bombă care explodează atunci când interacționează cu un foton. În ciuda dificultății depozitării unui astfel de aparat, să spunem că am reușit să stocăm o cantitate mare de astfel de bombe, așteptând să înceapă un conflict, dar, din fericire, acest conflict a putut fi evitat.
Între timp, pentru o parte dintre bombe, senzorul de lumină s-a stricat, ceea ce înseamnă că aceste bombe nu mai pot fi folosite, întrucât nu pot exploda (la trecerea unui foton prin acestea, nu se mai declanșează reacția ce duce la explozia bombei; dar, important, fotonul nu mai interacționează cu bomba în niciun fel).
Întrebarea este: cum putem afla ce bombe mai sunt funcționale? Bineînțeles, dacă nu ne interesează integritatea bombelor (și siguranța personală), am putea, pur și simplu, să le testăm cu un laser, iar cele care explodează vor fi cele funcționale. Dar în felul ăsta, când terminăm de efectuat testul, nu vom mai rămâne cu nicio bombă funcțională întreagă, pentru că au explodat.
Ar fi mai folositor să putem să le testăm fără să le detonăm pe cele funcționale. Asta ar fi ceva extraordinar! Dar este așa ceva posibil? Aici intervine „magia” mecanicii cuantice...
Interferometrul Mach-Zehnder
În 1993, Avshalom Elitzur și Lev Vaidman au publicat o lucrare în care analizează această problemă și oferă o soluție folosind aparatul descris mai jos.
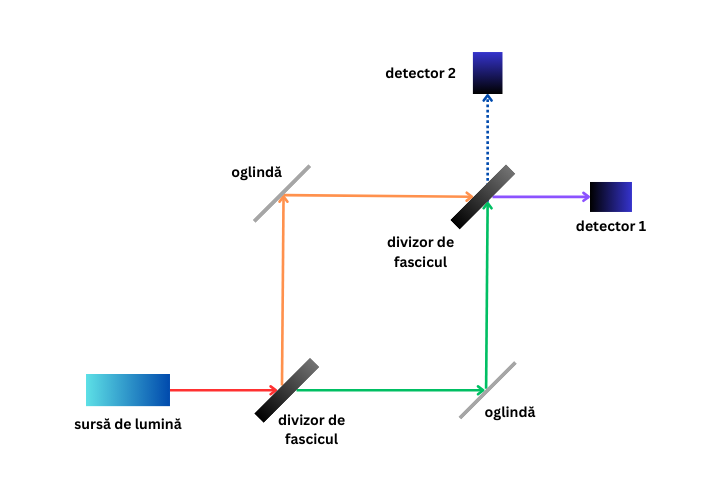
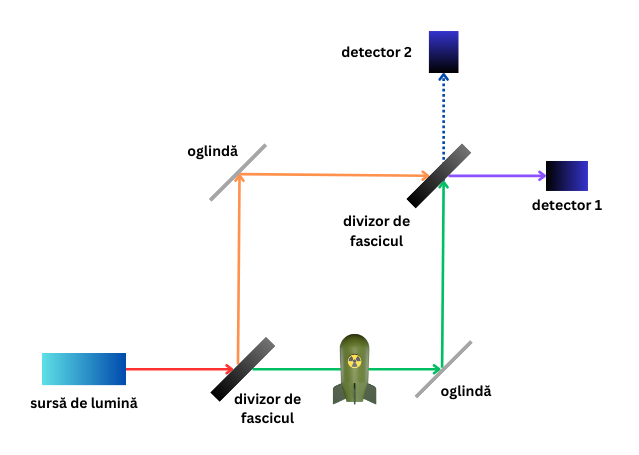
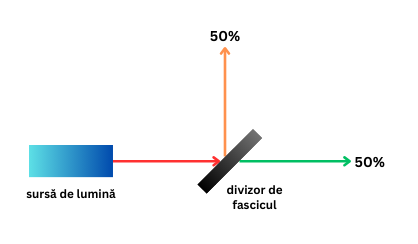
Acest aparat se numește interferometru Mach-Zehnder. Sursa de fotoni trimite un singur foton către primul divizor de fascicul. Când un foton ajunge la divizor, acesta are o probabilitate de 50% de a trece prin divizor și o șansă de 50% de a fi reflectat, nimic ieșit din comun.
Experimentul devine interesant atunci când fotonul trece de oglinzi și ajunge la al doilea divizor.
Intuiția ne spune că fotonul ori va trece prin divizorul al doilea, ori va fi reflectat, iar primul detector va observa fotonul in 50% din cazuri și al doilea tot in 50% din cazuri. După cum știm, însă, mecanica cuantică este rareori intuitivă.
Rezultatul experimental este că fotonul va fi detectat de primul aparat de măsură (detector 1) de fiecare dată.
Explicația? Fotonul a interferat cu el însuși.
Similar experimentului cu fantă dublă, când fotonul a trecut prin primul divizor de fascicul, acesta nu a urmat în mod exclusiv una dintre traiectorii, ci a fost plasat într-o superpoziție, deplasându-se astfel pe ambele traiectorii și întâlnindu-se cu el însuși la al doilea divizor unde, datorită anumitor proprietăți ale divizorilor (schimbare de fază în funcție de direcția din care vine fasciculul), a interferat constructiv pe traiectoria spre primul detector și distructiv pe traiectoria către cel de-al doilea, ca și cum ar fi fost doi fotoni, în loc de unul.
Faptul că divizorul doi asigură detectarea fotonului doar de către detectorul 1 este important! Se întâmplă asta dacă fotonul, aflat în superpoziție, se deplasează simultan pe ambele traiectorii! Dacă pe una dintre traiectorii apar probleme (survine o măsurătoare a fotonului), atunci acesta nu mai poate interfera cu sine la al doilea divizor și vom avea situații diferite, explicate mai jos.
Ce facem cu bombele?
Acum că înțelegem cum funcționează un interferometru Mach-Zehnder, cu ce ne ajută asta în a afla care bombe încă sunt funcționale, fără a le distruge?
Elitzur și Vaidman propun să punem bomba pe care vrem să o testăm pe una dintre traiectoriile dintre divizorii de fascicul. O plasăm, așa cum puteți observa în imaginea de mai sus, pe traiectoria de jos. Să vedem ce se întâmplă în această situație.
I. Să analizăm mai întâi situația în care bomba nu este funcțională.
Sursa de fotoni trimite un foton, acesta ajunge la divizor și are o probabilitate de 50% de a trece prin divizor, ajungând la bombă, și o probabilitate de 50% de a fi reflectat.
Totuși, întrucât bomba este nefuncțională, fotonul poate pur și simplu să treacă prin ea, ceea ce înseamnă că din „perspectiva” fotonului este ca și cum bomba nu ar exista, iar totul se va desfășura ca într-un interferometru Mach-Zehnder normal, superpoziția fiind neafectată până la al doilea divizor. Astfel, orice bombă nefuncțională pusă în aparat va avea ca rezultat un foton măsurat de primul detector.
II. Acum să vedem ce se întâmplă dacă bomba este funcțională.
După primul divizor, ca întotdeauna, fotonul se află într-o superpoziție, cu o probabilitate de 50% de a lua traiectoria de sus și 50% de a lua traiectoria de jos. Acum, însă, dacă fotonul ajunge la bombă, aceasta va exploda, iar experimentul va fi un eșec. Asta se întâmplă în jumătate din cazuri.
Dar dacă bomba nu a explodat, știm sigur că fotonul a luat drumul de sus. Astfel, superpoziția a fost distrusă înainte ca fotonul să ajungă la al doilea divizor de fascicul, ceea ce înseamnă că nu va exista niciun fel de interferență.
Când bomba este funcțională și fotonul ajunge la al doilea divizor, în 50% din cazuri fotonul va trece prin divizor, ajungând la primul detector, ceea ce nu ne oferă nicio informație despre starea bombei (este același rezultat cu cel oferit de o bombă nefuncțională), dar în cealaltă jumătate de cazuri, fotonul va fi reflectat, ajungând la al doilea detector și confirmând că bomba este funcțională fără a o atinge!
Așadar, și aceasta este probabil cheia înțelegerii întregului experiment: fotonul poate ajunge la detectorul al doilea doar în cazul în care a urmat traiectoria de sus și a fost reflectat către detectorul 2. Asta, din nou, se întâmplă în jumătate din cazurile în care fotonul se deplasează pe traiectoria de sus, pentru că în cealaltă jumătate trece prin divizor și ajunge în detectorul 1.
Din nou, în cazul în care fotonul nu interacționează cu bomba (este defectă), întotdeauna va merge către detectorul 1.
Doar în situația în care fotonul se deplasează pe traiectoria de sus, iar bomba este funcțională, putem avea situația (25% din cazuri) în care fotonul ajunge la detectorul al doilea. Și astfel știm că bomba este funcțională, deși fotonul nu trece prin aceasta! Mecanica cuantică la apogeul său 😃
În concluzie, când bomba este funcțională, în 50% din cazuri aceasta va exploda, în 25% (50% probabilitate de a nu trece pe la bombă x 50% probabilitate de a trece prin divizorul de fascicul) din cazuri vom obține același rezultat ca cel pentru o bombă nefuncțională, iar în 25% din cazuri vom știi cu certitudine că bomba este funcțională fără ca aceasta să fie detonată.
Nu par a fi probabilități extraordinare, dar prin modificarea experimentului, probabilitatea de a detona bomba poate fi îmbunătățită până când devine nesemnificativă. Dar chiar și în cazul în care probabilitatea de a verifica o bombă dacă este funcțională, fără a o detona, este de 25%, tot este mai bine decât în situația „prezisă” de fizica clasică, ce nu ne poate ajuta deloc.
Discuție și consecințe
Experimentul descris mai sus este un tip de măsurătoare fără interacțiune. Fără a știi ceva despre bombă și fără a interacționa cu ea, simpla ei existență duce la schimbări măsurabile ale rezultatelor experimentului.
Pare paradoxal, de parcă informația apare din nimic, însă interpretarea universurilor multiple a mecanicii cuantice pare să explice asta. Conform lui Elitzur și Vaidman, o interacțiune cu bomba are loc, doar că nu în universul nostru, iar, deoarece toate universurile se regăsesc în același omnivers, se poate spune că bomba a fost „atinsă”, în general.
Ați putea fi tentați să spuneți că există alte tipuri de măsurători fără interacțiune ce nu necesită o înțelegere a mecanicii cuantice. Un astfel de exemplu ar putea fi un experiment cu două cutii și o minge. Să presupunem că știm că mingea este într-una dintre cutii. Astfel, deschizând una dintre cutii, chiar dacă mingea nu este acolo (și, deci, nu interacționăm cu ea), știm clar în care dintre cutii se află mingea. Problema cu acest experiment este că avem deja informații despre obiectul pe care vrem să îl măsurăm, și anume că mingea este în mod clar într-una dintre cutii și nu altundeva în univers. Nu avem acces la astfel de informații în cazul bombelor noastre.

