La ce înălțime de sol se va situa o sfoară cu lungimea cu 1 m mai mare decât circumferința Terrei?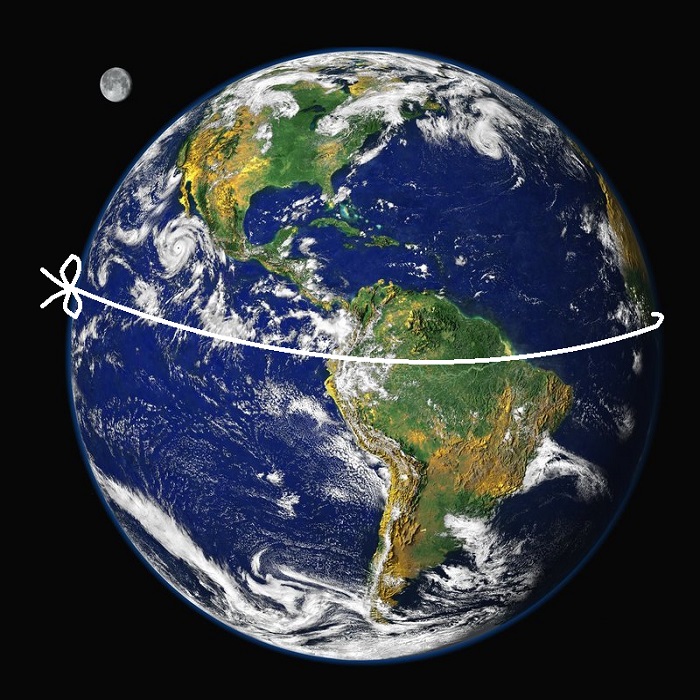
Priviţi imaginea de sus a Pământului. Să ne imaginăm că Pământul este perfect rotund la ecuator şi că legaţi o sfoară strâns în jurul acestuia, de-a lungul ecuatorului. Acum faceţi următoarea modificare: adăugaţi 1 metru de sfoară la sfoara care înconjoară Pământul. Sfoara a devenit, aşadar, mai lungă cu un metru. Ridicaţi acum sfoara, după adăugarea acelui metru suplimentar, în aşa fel încât aceasta să se afle la aceeaşi înălțime de suprafaţa terestră.
Care va fi înălţimea la care se va afla sfoara de suprafaţa terestră?
Iată patru variante de răspuns:
a) 0,0000001 mm
b) 1 mm
c) 15 cm
d) 1 m
V-aţi decis?
Mergeți în partea a doua a articolului pentru a vedea soluţia.
Până vă mai gândiți, iată o imagine tulburătoare cu planeta noastră, surprinsă din depărtările spațiului...

Credit imagine: NASA/JPL-Caltech/Space Science Institute.
În această imagine rară, obţinută în data de 19 iulie 2013, camera de fotografiat, având un obiectiv cu un unghi larg de vizualizare, aflată pe sonda spaţială Cassini a NASA, a surprins inelele planetei Saturn şi imaginea planetei Pământ, în acelaşi cadru.
OK? Ați dat un răspuns?
Iată răspunsul corect: c), 15 cm.
În fapt este foarte simplu de calculat.
Lungimea cercului = 2 • π • R
π = 3,14, R = raza Pământului = 6.371.000 metri
Dacă o să faceţi calculul, veți observa că lungimea cercului va fi 6.371.000 • 2 • 3,14 = 40,009,880 metri, care este, în fapt, lungimea sforii în jurul ecuatorului.
Adăugăm, aşa cum am spus, 1 metru la sfoară. Asta înseamnă că sfoara va avea: 40,009,880 + 1 = 40,009,881 metri.
Aplicăm din nou aceeaşi formulă: L = 2 • π • R, rezultă că R = L / (2 • π)
R = 40.009.881 (lungimea sforii, după adaosul de 1 metru) / (2 • π )= 6.371.000,15 m
Vedeţi, aşadar, că după adăugarea unui metru de sfoară, raza va fi mai mare cu 0,15 m, ceea ce înseamnă că aceasta va fi înălțimea la care va fi sfoara deasupra suprafeței terestre.
Problema cu intuiţia umană
Matematica aplicată este banală. Nu asta e de învăţat din acest articol, ci despre cât de greşită poate fi intuiţia umană câteodată...
De ce este atât de greșită intuiția noastră în acest caz? Greu de spus. Poate pentru că nu seamănă cu alte situații similare, când adăugăm numere mici la numere mari, cum ar fi: a) adăugarea unei picături într-un lac; b) adăugarea unui măr într-un camion de mere șamd. Acestea sunt situații în care un mic adaos nu produce o diferență vizibilă. Iar când ne gândim la dimensiunea enormă a lungimii ecuatorului, 1 metru adăugat nu pare să însemne mare lucru.
Am numit acest articol „Paradoxul...”, dar nu este vorba de niciun paradox, desigur. Poate părea paradoxal, pentru că este contraintuitiv, nimic mai mult.
Care este lecţia? Faptul că lumea în care trăim este complexă, cu multe necunoscute, iar de multe ori ceea ce „ni se pare” corect poate fi departe de adevăr, cum, probabil a fost în acest caz, când a trebuit să vă bazați pe propria intuiție pentru a ghici cât de departe va fi de suprafața terestră sfoara, după adaosul de 1 metru.
De multe ori ne formăm opinii pe date incomplete, pe „feeling”, pe „așa mi se pare”, „așa pare firesc/logic” șamd.
Acest exercițiu este, așadar, o invitație la umilință și... încredere în matematică :)
