Scientia

Pentru multă vreme, din cauza unei culturi total diferite de cea europeană, dar şi datorită autoizolației Chinei, matematica dezvoltată în această ţară a fost un adevărat mister pentru occidentali. În continuare, despre primele sisteme de numeraţie chinezeşti.

În Egiptul antic primele observaţii matematice au luat naştere datorită nevoii de a măsura terenurile după ce acestea erau inundate de Nil. În schimb, în China, primele cunoştinţe matematice s-au datorat astronomiei şi astrologiei. Astfel, la mijlocul mileniului 2 î.Hr., s-a început o descriere atât a constelaţiilor, cât şi a stelelor, ceea ce necesita calcule matematice pentru aflarea distanţei. După un avans în domeniul astronomiei, chinezii au adoptat în secolul 5 î.Hr. un calendar care avea 365 de zile.

În China primele inscripţii apar în secolele 16-11 î.Hr. pe oase sau pe carapace de broască ţestoasă, iar primele notaţii de numere apar şi sub formă de noduri, pe diferite funii (noduri pe coarde, cum se numeau). De-a lungul vremii, numeraţia chineză a cunoscut diferite variante. Se presupune că cifra „zero” a fost adusă din India, sub forma unui punct sau a unui cerculeţ, de către Gautama Siddha, astronom chinez de origine indiană.

Primul sistem de numeraţie chinez consta dintr-o serie de 13 hieroglife, 9 semne pentru unităţile de la 1 la 9 şi 4 semne pentru primele patru puteri ale lui 10. Traducerea acelor hieroglife ar fi  următoarea, cu denumirea chineză specifică:

Se observă că din seria de hieroglife lipseşte cifra 0, care încă nu era folosită. Numerele mai mari erau scrise folosind aceeaşi serie de 13 hieroglife.

Exemple:

11= 10 (shi) + 1 (yi) => 11 = shi yi
20= 2 (er) x 10 (shi) => 20 = er shi
100= 1 x 100 => 100 = yi bai

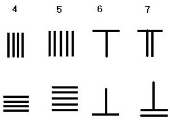
Pe lângă acest sistem de numeraţie, mai complicat, datorită faptului că hieroglifele aveau o grafie nu tocmai uşoară, chinezii mai foloseau un altul, numit suan-zi. Acest sistem de notare a numerelor era unul mult simplificat, cifrele fiind reprezentate prin beţişoare. El se realizează prin combinaţii simple de beţişoare, atât pe orizontală, cât şi pe verticală, ca în figura de mai jos:

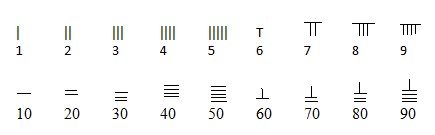
Şi din acest sistem de numeraţie care era folosit încă din secolul 2 î.Hr. lipseşte cifra 0. Acest sistem era folosit cu mare eficienţă în calculul cu beţişoare şi mai apoi în calculul cu abac ( socotitoarele din ziua noastră). Abacul era folosit şi în Japonia. Este de mirare ce performanţe a atins un japonez ce făcea calcule cu abacul. În noiembrie 1945, expertul japonez în abac Matzuzaki a concurat cu un expert în operarea cu calculatorul cel mai performant de la acea vreme. Întrecerea a constat în 5 probe în care cei doi trebuiau să execute în cel mai scurt timp şi fără greşeală mai multe operaţii aritmetice cu numere de 6-9 cifre. Japonezul a câştigat cu 4-1.

Dacă cel de-al doilea sistem de numeraţie prezentat ar fi conţinut cifra „zero” el ar fi coincis cu cel de astăzi. Cifra zero era înlocuită cu un spaţiu gol, însă asta producea confuzii deoarece acelaşi aranjament de beţisoare putea însemna mai multe numere.

Exemplu:

, putea să însemne atât 708, cât şi 7080, 70800 etc.

Mai apoi, s-a introdus şi simbolul O pentru zero care permite scrierea unor numere ca: 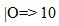sau 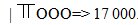 . Nu se ştie exact în ce secol a fost adusă cifra zero, dar se bănuieşte că între secolele 8-12.

Datorită barierelor de limbă, dar şi poziţionării geografice, se observă că matematica chineză s-a dezvoltat independent faţă de matematica altor popoare, iar influenţele şi-au făcut simţită prezenţa foarte greu.

Bibliografie:
“O istorie a matematicii”. Adrian C. Albu, Editura Nomina, 2009.