Universul nu este mecanic, ci este format din câmpuri de forță. Atunci când o antenă radio produce o perturbare a câmpurilor electrice și magnetice, aceste perturbații se deplasează spre exterior ca undele pe un iaz.

Undele sunt fundamentale pentru modul în care funcționează universul.
Scala radioului este calibrată în unități de frecvență, dar cel mai simplu exemplu al acestui concept este furnizat nu de o undă, ci de un obiect care vibrează, cum ar fi un obiect la un capăt al unui arc, 8. Fără forțe aplicate asupra acestuia, arcul are lungimea sa de echilibru, a/1. Poate fi întins (a/2) sau comprimat (a/3).
Atașăm arcul de un perete în stânga și de un obiect în dreapta. Dacă acum lovim obiectul cu un ciocan (a/4), aceasta oscilează așa cum se vede în seria de instantanee 4-13.
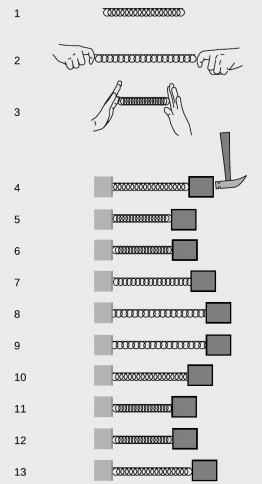
Figura a
Dacă presupunem că obiectul atașat de arc se deplasează înainte și înapoi fără frecare și că mișcarea este unidimensională, atunci conservarea energiei ne indică faptul că mișcarea trebuie să fie repetitivă. Când obiectul revine din nou la poziția sa inițială (7), energia sa potențială este din nou aceeași, deci trebuie să aibă din nou aceeași energie cinetică. Cu toate acestea, mișcarea este în direcția opusă. În cele din urmă, la 10, revine la poziția sa inițială cu aceeași energie cinetică și aceeași direcție de mișcare. Mișcarea a trecut printr-un ciclu complet și acum se va repeta pentru totdeauna dacă nu avem frecare.
Terminologia obișnuită pentru o mișcare care se repetă mereu este „mișcarea periodică”, iar timpul necesar unei repetări complete se numește „perioadă”, T.
Rapiditatea unei vibrații, dată de numărul de vibrații pe secundă, se numește „frecvență”, f. Perioada este numărul de secunde necesare pentru o mișcare completă (ciclu complet), iar frecvența este numărul de cicluri pe secundă.
Un Hertz, numit în onoarea unui pionier al tehnologiei radio, reprezintă un ciclu pe secundă. În formă prescurtată, 1 Hz = 1 s-1. Aceasta este unitatea familiară utilizată pentru frecvențele de pe scala de frecvențe a unui aparat radio.

Unitățile de frecvență sunt, de asemenea, utilizate în mod obișnuit pentru a specifica viteza computerelor. Toate circuitele de pe un cip de computer sunt sincronizate de un ceas electronic, astfel încât circuitele să poată coopera pentru îndeplinirea unei sarcini, fără a fi discrepanțe de timp. Adăugarea a două numere ar putea necesita, să zicem, 30 de cicluri de ceas.
Am discutat cum să măsurăm cât de repede vibrează ceva, dar nu cât de mari sunt vibrațiile. Termenul general pentru aceasta este „amplitudine”, A. Definiția amplitudinii depinde de sistemul discutat, iar două persoane care discută același sistem nu pot folosi aceeași definiție.
În exemplul obiectului atașat de arc, b / 1, amplitudinea va fi măsurată în unități de distanță, cum ar fi cm. S-ar putea lucra în funcție de distanța parcursă de obiect de la extrema stângă la extrema dreaptă, dar e mai întâlnit în fizică să se utilizeze distanța de la centru la o extremă. Primul este denumit de obicei amplitudinea vârf-la-vârf.
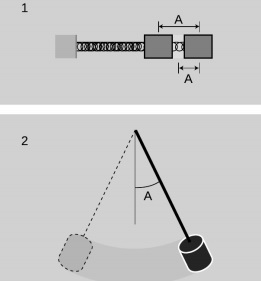
Imaginea b
În alte situații nu am folosi aceleași unități pentru amplitudine. Amplitudinea unui copil aflat pe un leagăn sau pe un pendul, b / 2, ar fi cel mai convenabil măsurată prin prisma unghiului, nu ca distanță, deoarece picioarele se vor deplasa la o distanță mai mare decât capul. Vibrațiile electrice ale unui receptor radio ar fi măsurate în unități electrice, cum ar fi volții sau amperii.
În multe exemple fizice de vibrații, forța ce readuce obiectul vibrator înapoi la echilibru devine din ce în ce mai puternică pe măsură ce obiectul se depărtează mai mult de echilibru, iar forța este direct proporțională cu distanța de echilibru. Majoritatea arcurilor se comportă astfel, așa că, de exemplu, ne-am aștepta ca arcul din figura a să ajungă la o forță dublă atunci când este întins de două ori mai mult.
Apoi definim o constantă, care ne spune câți newtoni de forță obținem pe un metru de întindere. De exemplu, Turnul John Hancock are o constantă de aproximativ 200 MN / m (meganewtoni pe metru), ceea ce înseamnă că vântul trebuie să exercite o forță de aproximativ 200 MN pentru a face turnul să se legene cu un metru. Pentru a-l face să se balanseze cu doi metri, forța ar trebui să fie de 400 MN.

Turnul John Hancock
Când forța are acest tip de comportament matematic, mișcarea rezultată este cunoscută sub numele de „mișcare armonică simplă”. Un fapt surprinzător și util despre mișcarea armonică simplă este că frecvența sa este independentă de amplitudine. Intuitiv, ne-am aștepta ca vibrațiile cu o amplitudine mai mare să dureze mai mult timp, adică să aibă o frecvență mai mică. Cu toate acestea, atunci când amplitudinea este mai mare, forța care accelerează masa înapoi către poziția de echilibru este, de asemenea, mai mare și acest lucru se dovedește a compensa exact nevoia de a parcurge o distanță mai mare.
Legenda spune că Galileo a observat acest fapt pentru prima dată când a privit un candelabru care se balansa în timpul slujbei bisericești și l-a cronometrat cu ajutorul pulsului său.
— ••• —
Acest articol este parte din cartea "Fizica conceptuală" de Benjamin Crowell
CUPRINS
8.1 Vibrațiile undelor
