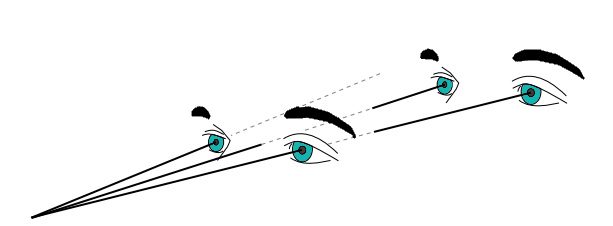
Paralaxa se înjumătățește odată cu dublarea distanței obiectului observat
În articolul precedent menționam că putem folosi luminozitatea (unei stele) pentru a determina distanța Dar sistemul vizual al omului dispune de o metodă diferită. De exemplu, poți spune chiar acum la ce distanță se află ecranul computerului ori telefonului pe care citești acest text. Senzația de adâncime vine de la faptul că cei doi ochi furnizează informații despre același lucru, dar din perspective (un pic) diferite. Dacă închizi și închizi pe rând cei doi ochi (unul închis, celălalt deschis), vei observa că imaginea se deplasează spre stânga, respectiv spre dreapta. Dacă nu crezi, interpune un deget între tine și ecran și observă cum un anumit punct de pe ecran se deplasează față de degetul tău.
Dacă te uiți la o muscă aflată pe nasul tău, va fi un unghi de aproape 180° între raza de lumină de la muscă la ochiul tău stâng și raza de lumină de la muscă la ochiul tău drept. Creierul va ști că acest unghi foarte mare înseamnă o distanță foarte mică. Acest unghi este numit unghiul paralaxei sau paralaxă.
Paralaxa este, așadar, unghiul dintre dreptele care unesc un punct foarte depărtat cu extremitățile unei baze de observare.
Obiectele aflate la distanțe mai mari au paralaxe mai mici, iar când unghiul este mic este o bună aproximare dacă spui că unghiul este invers proporțional cu distanța. În imaginea de mai sus unghiul este înjumătățit atunci când persoana se află la de două ori distanța la care s-a aflat inițial.
Dar paralaxa poate fi observată și în alte moduri decât cu o pereche de ochi. Pe când erai copil ai fost probabil uimit să observi că, aflat în deplasare, privind Luna, aceasta părea să te urmărească, să se deplaseze cu tine. Sigur, Luna nu te urmărea. Impresia de uimire avea la bază faptul că te așteptai, fără să știi detalii tehnice, ci intuitiv, să observi paralaxa, să observi o diferență pe măsură ce te deplasai și observai același lucru, Luna, din perspective diferite, așa cum se întâmplă, de exemplu, atunci când observi, în trecere, o casă aflată în apropiere.
Dar obiectele aflate la mare distanță au paralaxe foarte mici pentru a le observa atunci când te deplasezi. În general, razele care vin de la obiecte aflate la mare distanță sunt aproape paralele.
Dacă punctele folosite pentru comparație (cele din care observi) sunt la distanță suficient de mare, atunci paralaxa obiectelor depărtate poate fi observată. În secolul al XIX-lea nu se cunoștea cât de înalt este Himalaya ori unde anume, în mod precis, se află pe hartă vârfurile acestui lanț muntos. Se considera că Anzii sunt cei mai înalți munți de pe Terra. Nimeni nu ajunsese pe vârfurile cele mai înalte ale Himalayei. Din câmpiile Indiei nu se putea spune dacă e vorba de munți foarte înalți aflați la mare distanță ori mai mici, la distanță mai mică. Britanicul George Everest a stabilit adevărata distanță până la Himalaia și incredibila înălțime a vârfurilor sale observând vârfurile printr-un telescop din diferite locații.
O măsurătoare chiar mai spectaculoasă a fost efectuată de Hipparchus acum peste două mii de ani, măsurând paralaxa Lunii, având ca puncte de observare Alexandria și Hellenpond, stabilind că distanța până la satelit este de 90 de ori mai mare decât raza Pământului.
Paralaxa - folosind rotația planetei în jurul Soarelui

Steaua cea mai apropiată are un unghi (paralaxă) mai mare.
Terra orbitează Soarele. Ca urmare, putem determina distanța la câteva sute de stele prin măsurători la șase luni distanță (când Terra se află la mijlocul unei rotații complete, deci la distanța cea mai mare de poziția inițială).
În acest caz baza de observare pentru măsurarea paralaxei este diametrul orbitei Pământului. Pentru aceste stele distanțele determinate prin metoda paralaxei pot fi comparate cu cele determinate prin alte metode (prezentate aici).
— ••• —
Acest articol este parte din cartea "Fizica conceptuală" de Benjamin Crowell
CUPRINS
7.5 Utilizarea paralaxei pentru determinarea distanțelor
