În acest articol vom demonstra una dintre cele mai faimoase ecuații din matematică: ecuația lui Euler. Această egalitate este apreciată de mulți savanți (ca de exemplu, Richard Feynman) ca fiind o adevărată "bijuterie" matematică, întrucât combină cinci constante matematice fundamentale (,
,
și numerele 1 și 0), care par să fie din ramuri complet diferite ale matematicii, într-o singură ecuație simplă și elegantă.
Ecuația are următoarea formă:
unde este numărul lui Euler, baza logaritmului natural,
este unitatea imaginară, care satisface egalitatea
, iar
este raportul dintre circumferința unui cerc și diametrul său.
Pentru a demonstra această egalitate, vom avea nevoie să înțelegem mai întâi un alt concept matematic numit seria Maclaurin.
Să presupunem că vrem să aproximăm valoarea unei funcții, de exemplu funcția sinus (o vom nota f(x)), cu un polinom (notat p(x)).
Cea mai simplă aproximare ar fi ca polinomul nostru să aibă doar valoarea funcției f(x) la x = 0.
Atunci am avea polinomul
deci .
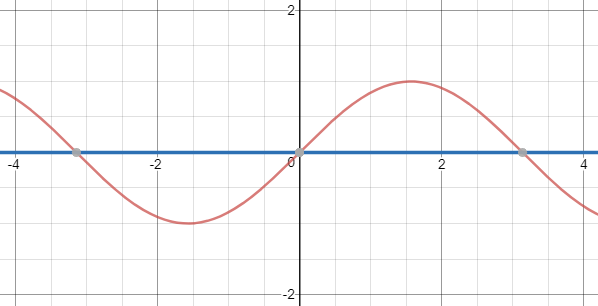
După cum puteți vedea, aceasta nu este o aproximare bună, întrucât aproximează doar un punct de pe funcția inițială.
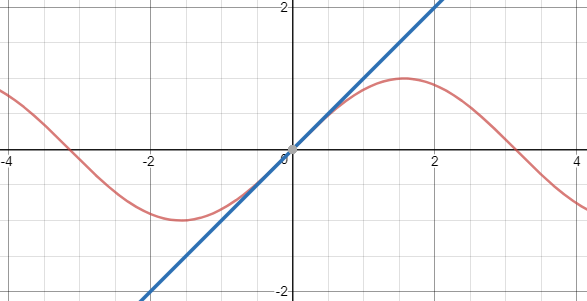
Să încercăm acum să facem polinomul să aibă și aceeași derivată de gradul 1 ca funcția sinus la x = 0 (derivata de gradul 1 al funcției sinus este funcția cosinus).
Atunci vom avea polinomul:
Putem verifica asta calculând:
și
Funcția sinus (în roșu) și aproximarea noastră (în albastru)
Această aproximare este în mod evident mai bună decât prima, întrucât aproximează mai multe puncte, deși este încă foarte departe de funcția adevărată.
Putem îmbunătăți aproximarea și mai mult, făcând și derivata de gradul 2 al polinomului să fie egală cu derivata de gradul 2 a funcției sinus, și derivata de gradul 3, și derivata de gradul 4 șamd.
Astfel vom obține o sumă infinită sub formă de polinom cu formula generală:
Această sumă infinită se numește o serie Maclaurin.
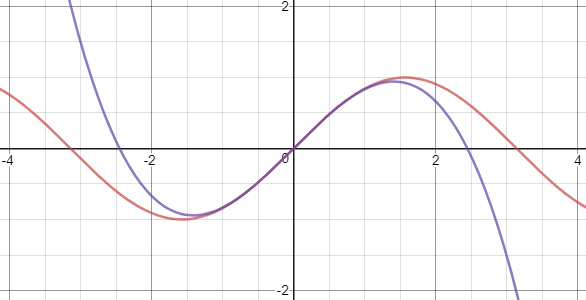
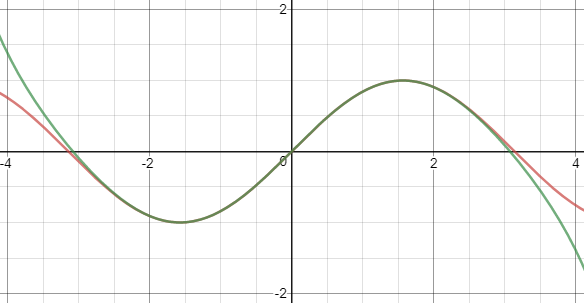
Funcția sinus (în roșu) și aproximarea folosind derivata de gradul 3 (în albastru)
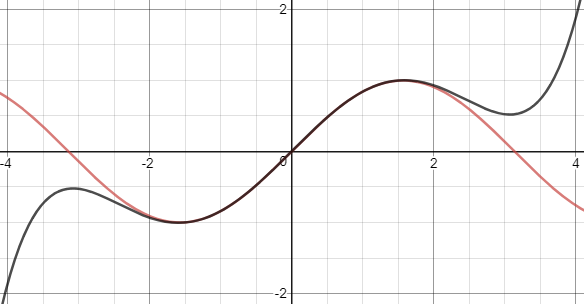
Funcția sinus (în roșu) și aproximarea folosind derivata de gradul 5 (în negru)
Acum că știim cum să calculăm o serie Maclaurin, vom calcula 3 astfel de serii: seria Maclaurin a funcției sinus , seria Maclaurin a funcției cosinus
și seria Maclaurin a funcției exponențiale
:
Pentru funcția sinus,
seria va repeta modelul la infinit, deci:
Pentru funcția cosinus,
seria va repeta modelul la infinit, deci:
Pentru funcția exponențială,
derivata funcției exponențiale va fi mereu funcția exponențială, deci toate derivatele vor avea valoarea e0 la x = 0, deci:
Acum că știm aceste serii Maclaurin, mai avem un lucru de făcut înainte de marele final.
Dacă înlocuim din funcția exponențială cu
(produsul dintre variabila
și unitatea imaginară), vom obține:
Această serie va repeta modelul .
Dacă separăm toți termenii fără coeficient de cei cu coeficient
și îl dăm pe
factor comun, vom avea:
După cum se poate vedea, prima paranteză este seria Maclaurin a funcției cosinus, iar a doua este seria Maclaurin a funcției sinus!
Putem înlocui parantezele cu funcțiile cosinus și sinus, respectiv pentru a obține formula lui Euler:
Înlocuind cu
obținem
deci, ecuația lui Euler: