 Mişcarea proiectilului. Galileo a fost inovator pe mai multe direcţii. El este, la limită, inventatorul software-ul open source. A inventat un dispozitiv mecanic de calcul pentru anumite aplicaţii inginereşti, dar a preferat să nu păstreze secret principiul dispozitivului, cum făceau rivalii lui, ci l-a făcut public. E drept, le lua bani celor care luau lecţii pentru a afla modul în care să-l folosească.
Mişcarea proiectilului. Galileo a fost inovator pe mai multe direcţii. El este, la limită, inventatorul software-ul open source. A inventat un dispozitiv mecanic de calcul pentru anumite aplicaţii inginereşti, dar a preferat să nu păstreze secret principiul dispozitivului, cum făceau rivalii lui, ci l-a făcut public. E drept, le lua bani celor care luau lecţii pentru a afla modul în care să-l folosească.
CUPRINS
2.3.4 Mişcarea în două dimensiuni
Pe de altă parte Galileo este şi primul fizician care a câştigat bani ca şi consultant militar. Galileo a înţeles proiectilele mai bine ca oricare altul, pentru că el a înţeles principiul inerţiei. Chiar dacă nu plănuiţi să aveţi o carieră în artilerie, mişcarea proiectilelor este un domeniul util de studiat, ocupându-se cu controlul mişcării în două sau trei dimensiuni.
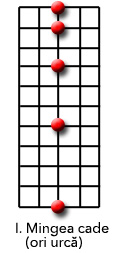
Figura i prezintă o minge în procesul de cădere sau urcare, nu are importanţă. Să spunem că mingea are o masă de un kilogram, fiecare pătrat din grilă are latura de 10 metri, iar poziţiile mingii sunt prezentate la intervale de o secundă. Forţa gravitaţională a Pământului exercitată asupra mingii este de 10 newtoni, deci la fiecare secundă impulsul mingii creşte cu 10 unităţi, iar viteza sa creşte cu 10 m/s. Mingea cade 10 m în prima secundă, 20 de m în a doua secundă şi aşa mai departe.
Auto-verificare: ce s-ar întâmpla dacă masa mingii ar fi fost de 2 kilograme?

j. Aceeaşi minge este văzută într-un sistem de referinţă în care se deplasează orizontal
Acum să ne uităm la mişcarea mingii dintr-un alt sistem de referinţă, j, care se mişcă cu 10 m pe secundă spre stânga în raport cu sistemul de referinţă utilizat în figura i. Un observator din acest sistem de referinţă vede mingea mişcându-se spre dreapta cu 10 metri pe secundă. Mingea formează un tip de arc de cerc, denumit în matematică parabolă:
1 pas lateral şi 1 pas jos
1 pas lateral şi 1 pas jos
1 pas lateral şi 1 pas jos
1 pas lateral şi 1 pas jos

k. Picăturile de apă se deplasează în arce parabolice
Nu contează care sistem de referinţă este cel „real”. Ambele diagrame arată mişcarea posibilă a unui proiectil. Lucrul interesant aici este că forţa gravitaţională, verticală, nu are nici un efect asupra mişcării orizontale, mişcarea pe orizontală nu are nici un efect asupra mişcării pe verticală. Cele două sunt complet independente. Dacă Soarele se află deasupra, mişcarea umbrei mingii pe sol pare perfect naturală: nu există forţe orizontale, aşa că fie este în repaus, fie se mişcă cu viteză constantă. (Forţă zero înseamnă o rată de transfer a impulsului egală cu zero). Acest lucru este adevărat şi dacă luminăm dintr-o parte şi plasăm umbra bilei pe un zid. Ambele umbre respectă legile fizicii.
Exemplul 12: Luna
În exemplul 12 v-am promis o explicaţie despre cum a ştiut Newton că valoarea câmpului gravitaţional „resimţit” de Lună (generat de Pământ) reprezintă 1/3600 din cel pe care-l „simţim” noi, aici, pe Pământ. Raza orbitei Lunii a fost cunoscută încă din Antichitate, deci Newton cunoştea viteza acesteia ca fiind de 1.100 m/s, exprimată în unităţi moderne.
Dacă gravitaţia Pământului nu ar acţiona asupra Lunii, aceasta ar zbura drept, de-a lungul liniei drepte reprezentate în figura l şi ar putea parcurge 1.100 m într-o secundă. Observăm însă că Luna descrie un arc de cerc având ca centru Pământul. Geometria ne arată că distanţa dintre arc şi linia dreaptă este de 1,6 milimetri. Lângă suprafaţa terestră, un obiect cade cu 5 metri într-o secundă, distanţă care este de 3.600 de ori mai mare decât 1,6 milimetri.
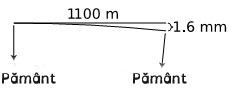
l. Traiectoria Lunii în raport cu Pământul
Partea confuză a acestui raţionament constă în faptul că deşi am spus că traiectoria proiectilului este o parabolă, în acest exemplu este un cerc. Ce se întâmplă? Ce este diferit aici este că atunci când Luna se mişcă cu 1.100 m/s îşi schimbă poziţia relativă faţă de Pământ, deci „în jos” este acum într-o nouă direcţie. Vom discuta în curând mai amănunţit despre mişcarea circulară, dar în acest exemplu, chiar nu contează. Curbura arcului este atât de lină că o parabolă şi un cerc par aproape identice. ( De fapt curbura este atât de lină - 1,6 milimetri la fiecare distanţă de 1.100 metri! - încât dacă aş desena figura la dimensiuni reale, nu aţi fi capabil să spuneţi că nu este dreaptă.)
Ca o interesantă notă istorică, Newton a susţinut că şi-a finalizat calculele referitoare la această problemă în timp ce se afla la ferma familiei sale, în timpul epidemiei de ciumă din 1666 şi a găsit rezultatele reprezintă „răspunsuri destul de precise”. Caietele sale arată însă că deşi el a efectuat calculele în aceea perioadă, rezultatele nu au ieşit suficient de exacte şi el a devenit nesigur cu privire la corectitudinea teoriei lui despre gravitaţie, dacă aceasta era corectă sau trebuia modificată. Abia în 1675 a intrat în posesia mai multor date astronomice, care l-au convins convins că teoria lui nu are nevoie să fie regândită. Se pare că el a rescris povestea vieţii lui parţial, cu scopul de a face să pară că munca lui a fost mult mai avansată în diverse momente, lucru care l-ar fi ajutat în disputa sa cu Leibniz asupra celui care a inventat analiza matematică.
