 Acum, există un amănunt extrem de subtil legat de pucul de hochei (vezi articolul precedent), care nu ar fi remarcat de majoritatea persoanelor. Dacă stăm pe gheaţă şi privim pucul nemişcăndu-se, înseamnă aceasta că este în repaus într-un mod absolut?
Acum, există un amănunt extrem de subtil legat de pucul de hochei (vezi articolul precedent), care nu ar fi remarcat de majoritatea persoanelor. Dacă stăm pe gheaţă şi privim pucul nemişcăndu-se, înseamnă aceasta că este în repaus într-un mod absolut?
Ţineţi minte, planeta Pământ se roteşte în jurul axei sale o dată la 24 de ore. La latitudinea unde trăiesc eu, aceasta înseamnă o viteză de aproximativ 800 de mile pe oră sau ceva în jurul a 400 de metri pe secundă. Am putea spune atunci că pucul nu se află în repaus cu adevărat. Am putea spune că pucul este de fapt în mişcare la o viteză de 400 m/s şi că îşi continuă mişcarea cu aceeaşi viteză. Aceasta ar putea părea că nu coincide cu descrierea de mai devreme, dar de fapt coincide. Din nou, nu este necesară cunoaşterea formulei energiei pentru a înţelege că dacă pucul îşi păstrează viteza (şi masa sa rămâne, de asemenea, aceeaşi), îşi păstrează energia.
Cu alte cuvinte, avem două sisteme de referinţă, ambele la fel de valide. Persoana ce stă pe gheaţă măsoară toate vitezele în funcţie de gheaţă şi găseşte viteza pucului că fiind şi rămânând zero şi spune că energia se conservă. Astronautul ce priveşte scena din spaţiul îndepărtat ar putea măsura viteza în funcţie de spaţia sa spaţială; în sistemul său de referinţă, pucul se mişcă cu o viteză de 400m/s, dar energia tot se conservă.

k / Avioanele sunt în repaus. Clădirea se mişcă.
Acestea par probabil lucruri de bun simţ, dar nu au fost aşa pentru una dintre cele mai inteligente persoane care a trăit vreodată, filosoful grec antic Aristotel. Acesta a imaginat un întreg sistem fizic pornind de la premisa că există un sistem de referinţă ce este special: pământul de sub picioarele noastre. Credea că orice mişcare are tendinţa de a încetini dacă nu există o forţa care să o menţină. Astăzi, ştim cu toţii că Aristotel s-a înşelat. O informaţie ce i-a lipsit a fost conceptul forţei de frecare. Dacă loviţi o minge de fotbal, motivul pentru care se opreşte până la urmă nu este că aşa vrea. Motivul este existenţa forţei de frecare a ierbii care o încetineşte (Energia cinetică a mingii se transformă în alte forme de energie, precum căldura şi sunetul.) Oamenii din ziua de astăzi ar putea remarca această greşeală mai uşor, pentru că avem experienţă cu mişcarea la viteze înalte. De exemplu, consideraţi un pasager al unui avion care se ridică şi din neatenţie îşi scapă punga cu alune. Conform lui Aristotel, punga s-ar oprit singură, devenind un proiectil mortal înăuntrul cabinei! În zilele noastre, cabina poate fi considerată în repaus.

j / De ce pare Aristotel atât de trist? Poate pentru că tocmai a realizat că toată fizica sa este greşită?
Galileo Galilei a fost primul fizician care a enunţat principiul inerţiei. Faptul că l-a contrazis pe Aristotel a avut consecinţe serioase. A fost interogat de autoritatea bisericească şi condamnat că preda faptul că Pământul se învârte în jurul Soarelui drept adevăr ştiinţific şi nu drept ipoteză matematică, după cum jurase. A fost pus sub arest permanent la domiciliu şi i-a fost interzis să scrie despre sau să îşi predea teoriile. La scurt timp a fost obligat să îşi retragă declaraţia cum că Pământul s-ar învârti în jurul Soarelui, dar se spune că, în schimb, a spus "şi totuşi se mişcă".

l / Galileo Galilei a fost primul fizician care a enunţat principiul inerţiei (deşi formularea diferă puţin de cea prezentată aici).
Principiul inerţiei spune, în mare, că toate sistemele de referinţă sunt în egală măsură valide.
Principiul inerţiei: rezultatele experimentelor nu depind de mişcarea rectilinie şi uniformă a dispozitivelor.
Pentru a fi ceva mai precişi, principiul inerţiei spune că în cazul în care obiectul B se mişcă rectiliniu şi uniform în funcţie de obiectul A, atunci obiectul B este la fel de valid ca şi obiectul A pentru a fi obiect de referinţă şi că un observator aflat lângă obiectul B va considera corpul B în repaus şi pe A în mişcare. Cineva aflat lângă corpul A va considera corpul B în mişcare.
Legile fizicii vor fi valide în ambele cazuri. Necesitatea unei formulări mai precise devine evidentă dacă vă gândiţi la exemplele în care mişcarea îşi schimbă viteza sau direcţia. Spre exemplu, dacă vă aflaţi într-o maşină ce accelerează de pe loc, vă veţi simţi împins înapoi pe scaun. Este foarte diferit de atunci când vă aflaţi în maşină şi aceasta deplasează cu aceeaşi viteză, când nu aveţi nicio senzaţie fizică. Un exemplu mai radical al acestora poate fi observat în figura de mai jos.
Exemplul 1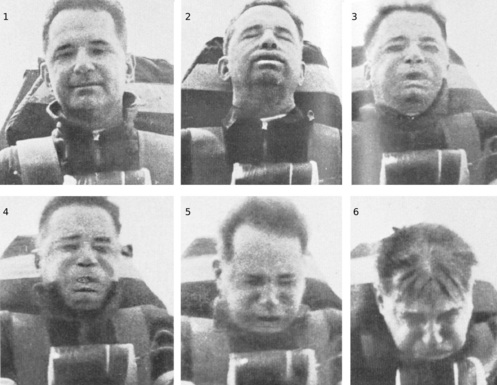
m / Acest doctor din cadrul Forţei Aviatice Militare s-a oferit voluntar pentru a conduce o sanie rachetă drept experiment medical. Efectele evident asupra capului şi feţei sale nu se datorează vitezei saniei, ci schimbărilor rapide ale vitezei acesteia: acceleraţie în 2 şi 3 şi deceleraţie în 5 şi 6. În 4 sania are viteza cea mai ridicată, dar pentru că este aproximativ constantă, doctorul nu este afectat la fel de tare.
Un sistem de referinţă aflam într-o mişcare rectilinie şi uniformă este cunoscut sub numele de sistem de referinţă inerţial, iar unul ce îşi modifică viteza sau direcţia mişcării se numeşte sistem de referinţă neinerţial. Principiul inerţiei se aplică doar sistemelor inerţiale. Sistemul de referinţă definit de o maşină aflată în acceleraţie este neinerţial, dar cel definit de o maşină ce se deplasează cu o viteză constantă este inerţial.
Exemplul 2: Pendulul lui Foucault
n / Foucault înfăţişându-şi unui public pendulul în 1851.
Mai devreme ne-am exprimat ca şi cum orice sistem de referinţă de pe suprafaţa Pământului, aflat în rotaţie, ar fi la fel de bun precum oricare altul. Acum, cu formularea mai exactă a principiului inerţiei, vedem că nu este chiar adevărat. Un punct de pe suprafaţa Pământului se mişcă în cerc, pe când principiul inerţiei se referă doar la mişcarea rectilinie. Cu toate acestea, curba mişcării este atât de lină încât în condiţii obişnuite nu remarcăm că sistemul de referinţă definit de pământul de pe jos nu este tocmai inerţial.
Prima demonstraţie a naturii neinerţiale a sistemelor de referinţă ataşate de sol a fost realizată de Léon Foucault utilizând un pendul foarte masiv (figura de mai sus) ale cărui oscilaţii persistau multe ore fără a deveni imperceptibile. Deşi Foucault a realizat demonstraţia la Paris, e mai uşor de imaginat ce s-ar întâmpla la Polul Nord: pendulul ar continua să se legene în acelaşi plan, dar Pământul s-ar roti sub el o dată la 24 de ore. Cuiva stând în zăpadă, i s-ar părea că planul de mişcare al pendulului se schimbă. Efectul la latitudine mai mici de 90 de grade se dovedeşte a fi mai lent, dar similar. Pendulul lui Foucault a fost prima dovada experimentală clară că Pământul se roteşte într-adevăr în jurul propriei axe, deşi oamenii de ştiinţă fuseseră convinşi de aceasta de peste un secol pe baza dovezilor indirecte legate de structura sistemului solar.
Oamenii sunt absolut convinşi că există o stare de repaus absolută şi că suprafaţa Pământului se află în această stare. Dar Copernicus a formulat presupunerea matematică, susţinută de Galileo pe baza fizicii, că Pământul s-ar învârti în jurul axei sale şi, de asemenea, în jurul Soarelui.
Opozanţii lui Galilelo au obiectat, susţinând că acest lucru ar fi imposibil, deoarece, dacă Pământul s-ar afla în mişcare, am observa efectele acelei deplasări. Au susţinut, spre exemplu, că dacă Pământul s-ar mişca, nu ar fi posibil să sari în aer şi să aterizezi în acelaşi loc – Pământul mişcându-se între timp sub tine. Galileo a realizat că aceasta nu era de fapt o neînţelegere legată de mişcarea Pământului, ci de fizică.
În una din cărţile sale, care a fost scrisă sub formă de dialoguri, sunt trei personaje care au o dezbatere asupra a ceea ce s-ar întâmpla dacă un marinar s-ar urca în vârful catargului unei corăbii plutind într-un port liniştit şi ar arunca de acolo o piatră. Ar lovi piatra puntea la baza catargului sau în spatele acestuia, deoarece corabia se va fi mişcat de sub aceasta? Acesta este tipul de experiment la care se face referire în principiul inerţiei, iar Galilelo ştia că rezultatul ar fi acelaşi indiferent de mişcarea navei. Raţionamentul opozanţilor săi, reprezentat de dialogul personajului nu foarte deştept Simplicio, se baza pe presupunerea că odată ce piatra pierde contactul cu mâna marinarului, începe în mod natural să îşi piardă mişcarea rectilinie. Cu alte cuvinte, nu erau de acord nici măcar cu idea că mişcarea continuă natural dacă nu acţionează asupra ei o forţă pentru a o opri.
Dar principiul inerţiei susţine mai multe de atât. Susţine că mişcarea nu este nici măcar reală: unui marinar aflat pe puntea corabiei, i se pare că puntea şi catargul şi velele nici măcar nu se mişcă. Oamenii de pe mal îi pot spune că nava şi propriul său corp se află într-o mişcare rectilinie şi uniformă. El va răspunde „Nu, aceea este o iluzie. Mă aflu în repaus. Singurul motiv pentru care credeţi că mă mişc este pentru că voi şi nisipul şi apa vă deplasaţi în direcţia opusă.” Principiul inerţiei spune că mişcarea rectiline şi uniformă este o problemă de opinie. Astfel lucrurile nu pot încetini „natural” şi să se oprească din mişcare, pentru că nu putem nici măcar să cădem de acord asupra căror obiecte se afla în mişcare şi care în repaus.
Dacă observatori în diferite sisteme de referinţă nu sunt de acord asupra vitezelor, este normal să dorească a efectua transformarea dintr-un sistem în altul. În cazul mişcării unidimensionale acest lucru este simplu de făcut, printr-o adunare.
Exemplul 3: Un marinar ce aleargă pe punte
Un marinar ce aleargă spre partea din faţă a corabiei, în sistemul de referinţă al celorlalţi marinari, puntea, are viteza de 7 m/s. Corabia se deplasează cu 1,3 m/s în funcţie de mal. Cât de repede va spune un observator de pe mal că se mişcă marinarul?
Vor spune că nava se deplasează cu 7 m/s şi că marinarul aleargă chiar mai repede, deoarece aleargă de la pupa la prora. Într-o secundă, corabia se deplasează cu 1,3 metri, dar el se mişcă cu 1,3+7 m, aşadar viteza sa faţă de plajă este de 8,3 m/s.
Singurul mod de a face această regulă să ducă la rezultate consistente este dacă definim vitezele de deplasare într-o direcţie ca şi pozitive, iar pe cele de deplasare în direcţia opusă ca şi negative.
Exemplul 4: Marinar ce aleargă în spate, către pupa
Marinarul din exemplul 3 se întoarce şi aleargă înapoi către pupa la aceeaşi viteză faţă de punte. Cum vor descrie matematic viteza sa ceilalţi marinari de pe corabie. Dar oamenii aflaţi pe plajă?
De vreme ce ceilalţi marinari au descris viteza lui ca fiind pozitivă prima oară, pe aceasta vor trebui să o considere negativă. Vor spune că viteza sa este acum -7 m/s. O persoană de pe mal va spune că viteza sa este 1,3+(-7)=-5,7 m/s.
— ••• —
Acest articol este parte din cartea "Fizica conceptuală" de Benjamin Crowell
CUPRINS
1.4.b. Principiul energiei
