
Ideea e prin inductie ,pentru inceput sa aratam ca relatia e adevarata pentru triunghi,dar voi arata intai ca e adevarata pentru un paralelogram.
Sa remarcam totusi ca relatia e adevarata pentru un dreptunghi cu laturile paralele cu axele.LA fel se remarca si pentru un triunghi dreptunghic cu catetele paralele cu axele fiind in fapt jumatatea unui dreptunghi ,nu e foarte greu avem in principiu 2 situatii ,prima in care diagonala imparte punctele interioare in doua sau in care o parte din punctele interioare devin puncte pe latura.
Sa presupunem ca pe diagonala se afla k puncte din cele interioare dreptunghiului astfel punctele interioare din triunghi devin (i-k)/2 in timp ce punctele de pe laturi creste cu k astfel avem g/2+k si se remarca ca noile valori verifica formula si reprezinta jumate din aria dreptunghi.
In figura avem un paralelogram care arie se deduce ca fiind aria unui dreptunghi din care se scad 4 triunghiuri drepte si la care cunoastem ca se aplica formula.Si daca numaram punctele interioare si cele de pe laturi de pe dreptunghi si triunghiri prin aceasta operatie obtinem si verificam aria paralelogramului.Asemanator cu triunghiul ca jumatate de dreptunhi ,deducem astfel ca formula e adevarata pentru un triunghi oarecare care este o jumatate de paralelogram.
Acum demonstratia fie un poligon Q cu n varfuri n>3 .Acest poligon sa poate forma din un poligon P si un triunghi T unind trei varfuri consecutive necoliniare. Presupunem prin inductie ca aria e verificata pentru poligoane cu un numar de varfuri mai mici decat n si vom arata ca e valabila formula si pentru n.Deci aria lui P si T verifica formula o sa notam cu 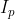 ,
,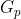 si
si 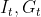 punctele interioare si de pe laturi ale triunghiului .Fie k numarul de puncte de pe latura comuna dintre P si T dar fara varfurile comune .
punctele interioare si de pe laturi ale triunghiului .Fie k numarul de puncte de pe latura comuna dintre P si T dar fara varfurile comune .
numarul I de puncte interioare a lui Q este

iar cele de laturile lui Q sunt  se scade de 2 ori deoarece acele k puncte nu vor mai fi pe latura si mai scadem 2 deoarece numaram de 2 ori cele 2 varfuri comune.
se scade de 2 ori deoarece acele k puncte nu vor mai fi pe latura si mai scadem 2 deoarece numaram de 2 ori cele 2 varfuri comune.
Aria lui Q este aria lui P plus aria ui T adica:
Acuma mai aramane sa vedem ca reprezinta exact formula pentru Q

Se vede imediat egalitatea (1)=(2) si cu asta am demonstrat inductia aratand ca relatia e adevarata si pentru n varfuri.