 Apa saturată de carbonat de calciu (sau alte minerale în unele cazuri) se scurge încet pe pereţii peşterilor. Evaporarea apei lasă în urmă doar mineralul, care în timp se adună şi formează depozite. Când acest lucru se întâmplă cu apa ce curge din tavan, apar stalactitele.
Apa saturată de carbonat de calciu (sau alte minerale în unele cazuri) se scurge încet pe pereţii peşterilor. Evaporarea apei lasă în urmă doar mineralul, care în timp se adună şi formează depozite. Când acest lucru se întâmplă cu apa ce curge din tavan, apar stalactitele.
- Detalii
- Scris de: Gabriela Costache
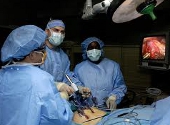 Încă din cele mai vechi timpuri, omul a simțit o atracţie pentru cunoașterea propriului corp. El a fost dintotdeauna conştient de necesitatea asistării la o naştere sau tratarea unei răni, căci aceste lucruri asigurau atât salvarea de vieţi, cât şi o perpetuare a speciei.
Încă din cele mai vechi timpuri, omul a simțit o atracţie pentru cunoașterea propriului corp. El a fost dintotdeauna conştient de necesitatea asistării la o naştere sau tratarea unei răni, căci aceste lucruri asigurau atât salvarea de vieţi, cât şi o perpetuare a speciei.
- Detalii
- Scris de: Irina Delia Duceac
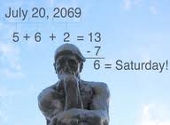 Cunoaşteţi persoane care pot calcula în ce zi a săptămânii cade o anumită dată, din trecut sau viitor, indiferent cât de îndepărtată în timp e data respectivă? Aflaţi că pentru a vă uimi şi dumneavoastră prietenii astfel este necesar să stăpâniţi doar câteva trucuri mentale simple.
Cunoaşteţi persoane care pot calcula în ce zi a săptămânii cade o anumită dată, din trecut sau viitor, indiferent cât de îndepărtată în timp e data respectivă? Aflaţi că pentru a vă uimi şi dumneavoastră prietenii astfel este necesar să stăpâniţi doar câteva trucuri mentale simple.
- Detalii
- Scris de: Adam Pash
 Vom continua în cele ce urmează cu prezentarea altor câteva invenţii trăsnite, de care cel mai probabil nu aţi auzit până acum. Vă invităm să citiţi despre chiloţii anticelular, uscătorul special de sutiene, păpuşa-calmant sau colacul de toaletă cu cântar încorporat.
Vom continua în cele ce urmează cu prezentarea altor câteva invenţii trăsnite, de care cel mai probabil nu aţi auzit până acum. Vă invităm să citiţi despre chiloţii anticelular, uscătorul special de sutiene, păpuşa-calmant sau colacul de toaletă cu cântar încorporat.
- Detalii
- Scris de: Irina Delia Duceac
 Dacă aveţi obiecte din argint sau placate cu argint, ştiţi bine că, în timp, suprafaţa strălucitoare va deveni mată şi întunecată. Acest lucru se întâmplă pentru că au loc reacţii între argint şi substanţele ce conţin sulf din aer. Cum facem argintul să strălucească din nou?
Dacă aveţi obiecte din argint sau placate cu argint, ştiţi bine că, în timp, suprafaţa strălucitoare va deveni mată şi întunecată. Acest lucru se întâmplă pentru că au loc reacţii între argint şi substanţele ce conţin sulf din aer. Cum facem argintul să strălucească din nou?
- Detalii
- Scris de: Gabriela Costache
 O definiţie mai restrânsă a roboticii ar suna astfel: "ştiinţa care se ocupă cu tehnologia, designul şi fabricarea roboţilor", însă această ramură a tehnicii este foarte complexă, necesitând cunoştinţe de electronică, mecanică şi programare.
O definiţie mai restrânsă a roboticii ar suna astfel: "ştiinţa care se ocupă cu tehnologia, designul şi fabricarea roboţilor", însă această ramură a tehnicii este foarte complexă, necesitând cunoştinţe de electronică, mecanică şi programare.
- Detalii
- Scris de: Irina Delia Duceac
 De-a lungul istoriei, descoperirile şi invenţiile ştiinţifice au schimbat cursul omenirii. Unele invenţii ca roata, avionul, automobilul, cauciucul, masele plastice sau tiparul au fost perfecţionate cu trecerea timpului şi le utilizăm sau cel puţin le vedem în fiecare zi.
De-a lungul istoriei, descoperirile şi invenţiile ştiinţifice au schimbat cursul omenirii. Unele invenţii ca roata, avionul, automobilul, cauciucul, masele plastice sau tiparul au fost perfecţionate cu trecerea timpului şi le utilizăm sau cel puţin le vedem în fiecare zi.
- Detalii
- Scris de: Irina Delia Duceac
Suntem singuri? Această întrebare este la fel de veche precum umanitatea însăşi. De milenii oamenii şi-au îndreptat privirea către stele şi s-au întrebat dacă undeva acolo există şi alte fiinţe asemenea lor. Viaţa, similară cu a noastră sau nu, există şi în alt loc din sistemul nostru solar? Dar în galaxia noastră?
Până în 1992, când existenţa primei exoplanete a fost confirmată, era incert dacă mai există şi alte planete în afara celor din sistemul nostru solar. Astăzi ştim de existenţa a peste 1000 de planete şi planete candidat care orbitează alte stele. Îndeplinesc aceste planete condiţiile necesare dezvoltării vieţii? Ce condiţii favorizează formarea de planete terestre în cursul dezvoltării sistemului planetar? NASA poate contribui la soluţionarea acestor probleme prin dezvoltarea misiunilor create să găsească şi să caracterizeze sistemele planetare.
Înainte de a determina dacă e vorba de sisteme planetare capabile să sprijine apariţia şi dezvoltarea vieţii, trebuie să le găsim. NASA Science urmăreşte acest scop prin sprijinirea mai multor eforturi independente efectuate la sol şi prin dezvoltarea misiunii Kepler, un telescop spaţial dedicat identificării şi determinării gradului de răspândire (numărului de planete care însoţesc de obicei o stea) a planetelor extrasolare.
Textul de mai sus reprezintă traducerea articolului What-are-characteristics-planetary-systems-orbiting-other-stars-and-do-they-harbor-life publicat de science.nasa.gov.
Traducere: Anamaria Spătaru
- Detalii
- Scris de: NASA

Nu numai că timpul este unul din marile mistere, dar în acelaşi timp deţine cheia pentru rezolvarea celei mai ambiţioase provocări din fizica teoretică, aceea de a cuprinde complexa lucrare a acestui vast univers într-o singură şi elegantă teorie: teoria totului.
- Detalii
- Scris de: Amanda Gefter
 Vă propunem astăzi un experiment de realizat acasă cu baloane de săpun. Toţi ne-am distrat la un moment dat făcând baloane de săpun. Din păcate, acestea, dacă nu sunt purtate de vânt, vor cădea şi la atingerea cu solul sau diverse obiecte se vor sparge.
Vă propunem astăzi un experiment de realizat acasă cu baloane de săpun. Toţi ne-am distrat la un moment dat făcând baloane de săpun. Din păcate, acestea, dacă nu sunt purtate de vânt, vor cădea şi la atingerea cu solul sau diverse obiecte se vor sparge.
- Detalii
- Scris de: Gabriela Costache
 Ce este timpul? Aceasta este o întrebare care a preocupat unele dintre cele mai mari minţi ale lumii, încă de la filozofii antici, până la oamenii de ştiinţă ai Iluminismului şi chiar şi după acesta. Are ştiinţa modernă un răspuns clar privind natura timpului?
Ce este timpul? Aceasta este o întrebare care a preocupat unele dintre cele mai mari minţi ale lumii, încă de la filozofii antici, până la oamenii de ştiinţă ai Iluminismului şi chiar şi după acesta. Are ştiinţa modernă un răspuns clar privind natura timpului?
- Detalii
- Scris de: Stuart Clark
 Sateliţii artificiali sunt corpuri construite de om şi apoi lansate în spaţiu, ce se deplasează pe o orbită în jurul Terrei şi care au rol în industria comunicaţiilor, dar şi în cercetarea ştiinţifică, atât a planetei noastre, cât şi a Universului. În continuare, o scurtă istorie.
Sateliţii artificiali sunt corpuri construite de om şi apoi lansate în spaţiu, ce se deplasează pe o orbită în jurul Terrei şi care au rol în industria comunicaţiilor, dar şi în cercetarea ştiinţifică, atât a planetei noastre, cât şi a Universului. În continuare, o scurtă istorie.
- Detalii
- Scris de: Irina Delia Duceac
 Vă invităm să citiţi în continuare povestea fascinantă a lui Yuri Gagarin, un erou rus plin de optimism şi care a ajuns să fie admirat de întreaga lume. La final veţi înţelege de ce toată lumea îl iubeşte pe Yuri Gagarin, primul om care a ajuns în spaţiu.
Vă invităm să citiţi în continuare povestea fascinantă a lui Yuri Gagarin, un erou rus plin de optimism şi care a ajuns să fie admirat de întreaga lume. La final veţi înţelege de ce toată lumea îl iubeşte pe Yuri Gagarin, primul om care a ajuns în spaţiu.
- Detalii
- Scris de: Jesus Diaz
 Când cerul este senin, se vede albastru. La răsărit şi la apus însă, culoarea cerului va fi diferită, având diferite nuanţe, în special o nuanţă roşiatică. Vom încerca în experimentul următor să ne fabricăm propriul cer senin, în miezul zilei şi la apus.
Când cerul este senin, se vede albastru. La răsărit şi la apus însă, culoarea cerului va fi diferită, având diferite nuanţe, în special o nuanţă roşiatică. Vom încerca în experimentul următor să ne fabricăm propriul cer senin, în miezul zilei şi la apus.
- Detalii
- Scris de: Gabriela Costache
Ce ne-am propus în acest articol este o sarcină relativ simplă: crearea unei liste cu site-urile care oferă un dicţionar al limbii române. În principiu cam toată lumea cunoaşte site-ul dexonline.ro. Dar acesta nu este singurul site care oferă un dicţionar al limbii române. Şi nu toate site-urile care oferă un dicţionar al limbii române folosesc baza de date construită de dexonline.ro.
Iată mai jos o listă a site-urilor care oferă dicţionarul limbii române şi o scurtă prezentare a acestora.
- Detalii
- Scris de: Iosif A.
