Cazul a=7 a fost analizat de Puiu in problema anterioara.
Se stie ca un patrat nu se poate termina in 2,3,7 sau 8 astfel se elimina cazurile a=3,8 4 sau 9.Mai raman cazurile de studiat a=1,2,5 si 6
Relatia data se poate scrie :
Pentru a=2 se remarca ca expresia este patrat perfect pentru orice n.
Sa remarcam si faptul ca expresia data e patrat perfect daca numaratorul e patrat perfect.
Pentru a=1 numaratorul se scrie 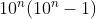 care este produs de numere consecutive si se stie (cultura!!!) ca produsul a doua numere consecutive nu e patrat perfect.Se arata usor cu n(n+1) ca este intre patratul lui n si n+1..
care este produs de numere consecutive si se stie (cultura!!!) ca produsul a doua numere consecutive nu e patrat perfect.Se arata usor cu n(n+1) ca este intre patratul lui n si n+1..
Pentru a=5 se arata ca numaratorul este situat intre patratele lui
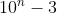 si
si 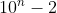 deci nu poate fi patrat perfect.
deci nu poate fi patrat perfect.
La fel si cazul a=6 numaratorul e incadrat de patratele lui
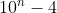 si
si 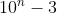 ..
..
Si cred ca am epuizat toate cazurile .Deci raspunsul este pentru a=2 si orice n,iar a=7 doar n=1 convine.