 Forţa reprezintă rata de transfer al impulsului. Echivalentul în cazul momentului cinetic se numeşte momentul forţei. Dacă forţa ne spune cât de tare apăsam sau împingem ceva, momentul forţei indică cât de tare răsucim acel ceva. Aţi avut vreodată experienţa de a încerca să deschideţi o uşă împingând în partea de lângă balama? Este greu de făcut, ceea ce indică faptul că o cantitate dată de forţă produce mai puţin moment al forţei când este aplicată în apropiere de axa de rotaţie.
Forţa reprezintă rata de transfer al impulsului. Echivalentul în cazul momentului cinetic se numeşte momentul forţei. Dacă forţa ne spune cât de tare apăsam sau împingem ceva, momentul forţei indică cât de tare răsucim acel ceva. Aţi avut vreodată experienţa de a încerca să deschideţi o uşă împingând în partea de lângă balama? Este greu de făcut, ceea ce indică faptul că o cantitate dată de forţă produce mai puţin moment al forţei când este aplicată în apropiere de axa de rotaţie.
CUPRINS
3.2 Momentul forţei
Momentul forţei = cantitatea de moment cinetic transferat / timpul necesar transferului
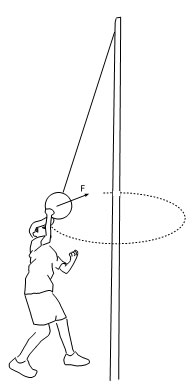
e. Băiat ce creează un moment al forţei lovind mingea de baschet
Pentru a încerca să fixăm această relaţie mult mai precis, să ne imaginăm că lovim o minge de baschet (în cadrul unui joc de tetherball). Băiatul aplică o forţă F mingii pentru o scurtă perioadă de timp t, accelerând mingea către o viteză v. Din moment ce forţa este rata de transfer al impulsului, avem F = mv/t , înmulţind în ambele părţi cu r, va rezulta Fr = mvtr.
Dar ± Fr este pur şi simplu valoarea momentului cinetic dat de minge, astfel încât ± mvr / t este egal, de asemenea, cu suma momentului forței pe care a aplicat-o. Rezultatul acestui exemplu este
Momentul forței = ± Fr
unde semnul plus sau minus indică dacă momentul forţei tinde să creeze mişcare în sensul acelor de ceasornic sau în sens invers. Această ecuaţie se poate aplica şi mai general, cu menţiunea că F ar trebui să includă doar acele părţi din forţă perpendiculare pe raza liniei.
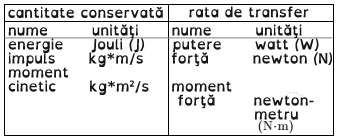
Pentru a rezuma, am învățat trei mărimi care se conservă, fiecare dintre ele având o rată de transfer
Momentul forţei se diferenţiază de forţă
Desigur, o forţă este necesară pentru a crea un moment al forţei (nu poţi răsuci un şurub fără a împinge cheia), dar forţa şi momentul forţei sunt două lucruri diferite. O deosebire între ele este direcţia. Noi folosim semne pozitive şi negative pentru a reprezenta forţele în cele două direcţii posibile de-a lungul unei linii. Direcţia momentului forţei nu este liniară, ci în sensul acelor de ceasornic sau invers.
Altă diferenţă între momentul forţei şi forţa este următoarea: o forţă aplicată mânerului uşii va schimba momentul cinetic al acesteia de două ori mai rapid decât în cazul în care forţa este aplicată la jumătatea distanţei dintre mâner şi balama. Aceeaşi forţă aplicată produce diferite mărimi ale momentului forţei în aceste două cazuri.
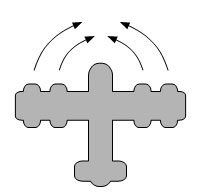
f. Cele patru motoare ale avionului produc un moment al forţei egal cu zero
Este posibil să aibă un moment al forţei total egal cu zero, având totodată o forţă totală diferită de zero. Un avion cu patru motoare cu reacţie (imaginea f) ar putea fi proiectat astfel încât forţele motoarelor să fie echilibrate atât pe stânga, cât şi pe dreapta. Forţele lor sunt toate orientate în aceeaşi direcţie, dar momentul forţei orientat în sensul acelor de ceasornic al două dintre motoare este anulat de către momentul forţei orientat invers acelor de ceasornic al celorlalte două motoare, conducând la un moment al forţei total egal cu zero.
În schimb, putem avea forţă totală zero si un moment al forței total diferită de zero. Motorul unui carusel are nevoie sa furnizeze un moment al forței diferit de zero pentru a putea atinge viteză , dar forța totală este zero. În cazul în care forța totală nu ar fi fost zero, centrul său de masă ar accelera!
Exemplul 5: Pârghia
Figura g prezintă un exemplu de o pârghie înăuntrul braţului tău. Diferiţi muşchi sunt utilizaţi pentru a flexa şi a întinde braţul , deoarece muşchii lucrează doar prin contracţii. Bicepşii flexează braţul.
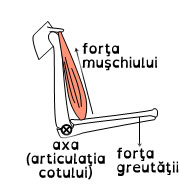
g. Bicepşii flexează braţul
Există trei forţe care acţionează asupra antebraţului: forţa venită de la biceps, forţa de la nivelul articulaţiei cotului şi forţa unei greutăţi ridicate. Deoarece articulaţia cotului este nemişcată , este firesc să se definească momentul forţei folosind articulaţia ca axă. Situaţia devine acum destul de simplă pentru că forţa osului braţului exercitată la nivelul cotului are r = 0 şi, prin urmare, nu creează niciun moment al forţei. O putem ignora complet. În general, am numi acest loc, punctul de sprijin al pârghiei.
Dacă ne-am limita la cazul în care antebraţul se roteşte cu un moment cinetic constant, atunci ştim că momentul forţei total al antebraţului este zero, astfel încât momentele forţei de la muşchi şi greutatea trebuie să fie opuse în semn şi egale în valoare absolută:
r muşchi F muşchi = r greutate F greutate
unde rmuşchi , distanţa de la articulaţia cotului către punctul de inserare al bicepsului de pe antebraţ, este de doar câţiva centimetri, în timp ce rgreutate poate avea în jur de 30 de centimetri. Forţa exercitată de muşchi trebuie prin urmare să fie de zece ori mai mare decât forţa exercitată de greutate. Vedem , astfel, ca această pârghie reduce forţa. În general, o pârghie poate fi utilizată fie pentru a creşte, fie pentru a reduce o forţă.
De ce au evoluat braţele noastre, astfel încât să ducă la reducerea forţei? În general corpul nostru este construit astfel încât să fie compact şi pentru o viteză de mişcare maxima, nu pentru o forţă maximă. Aceasta este principala diferenţă anatomică dintre noi şi neandertalieni (creierele lor aveau aceleaşi dimensiuni ca cele ale oamenilor moderni) şi pare să fi funcţionat pentru noi.
Precum şi în cazul tuturor celorlalte maşinării, pârghia este incapabilă să schimbe cantitatea de lucru mecanic pe care noi îl putem efectua. O pârghie care creşte forţa va reduce întotdeauna mişcarea şi vice-versa, lăsând lucrul mecanic neschimbat.
Teorema momentului cinetic a lui Noether
Să presupunem că o planetă fără soare stă singură într-un spaţiu interstelar, fără să se rotească. Apoi, într-o zi, începe să se învârtă. Acest lucru nu încalcă neapărat conservarea energiei, deoarece ar putea avea energie stocată, un exemplu este căldura din nucleul lichid ce poate fi transformat în energie cinetică. Într-adevăr încalcă conservarea momentului cinetic; dar chiar dacă nu am şti despre această lege a fizicii, povestea tot ar părea ciudată. Cum s-ar putea decide în jurul cărei axe să se învârtă?
Dacă ar începe să se învârtă în mod spontan în jurul unei axe, atunci aceea ar trebui să fie o direcţie specială, preferată din spaţiu. Aceasta înseamnă ca spaţiul însuşi ar trebui să aibă o asimetrie.
În realitate, aşa cum am menţionat anterior, experimentele arată, cu un grad foarte ridicat de precizie, că legile fizicii sunt simetrice raportate la diferite direcţii. Povestea planetei care începe brusc să se învârtă este un exemplu al teoremei lui Noether aplicată momentului cinetic. În continuare avem trei exemple asemănătoare:
| Simetrie | Cantitate conservată |
| Simetria timpului | masa-energie |
| Simetria de translaţie | impuls |
| Simetria de rotaţie | momentul cinetic |
