 “Sigur, şi poate mâine Soarele nu va mai răsări”. Desigur Soarele răsare şi apune doar pentru că Pământul se învârte, aşa că această expresie ar trebui să se refere la faptul improbabil că Pământul se va opri brusc din mişcarea sa de rotaţie în jurul propriei axe în timpul nopţii. De ce nu se poate opri? Nu ar încălca conservarea impulsului, deoarece rotaţia Pământului (în jurul axei sale) nu adăugă nimic impulsului său.
“Sigur, şi poate mâine Soarele nu va mai răsări”. Desigur Soarele răsare şi apune doar pentru că Pământul se învârte, aşa că această expresie ar trebui să se refere la faptul improbabil că Pământul se va opri brusc din mişcarea sa de rotaţie în jurul propriei axe în timpul nopţii. De ce nu se poate opri? Nu ar încălca conservarea impulsului, deoarece rotaţia Pământului (în jurul axei sale) nu adăugă nimic impulsului său.
CUPRINS
3.1 Momentul cinetic
În timp ce California se roteşte într-o anumită direcţie, o parte egală din India se roteşte în direcţie opusă anulând impulsul acestuia. O oprire a Pământului din rotaţia sa ar presupune o scădere a energiei cinetice, dar acea energie ar fi convertită simplu într-o altă formă, precum căldura.
Alte exemple pe această temă nu sunt greu de găsit. Un atom de hidrogen se învârte cu aceeaşi viteză de milioane de ani. Un săritor de la înălţime în apă cu experienţă care se roteşte după ce părăseşte platforma de lansare nu are nevoie să facă efort fizic pentru a continua mişcarea de rotaţie şi, într-adevăr, ar fi în imposibilitatea de a opri mişcarea de rotaţie înainte de a lovi apa.
Aceste observaţii au semnele distinctive ale unei legi de conservare, dar ce măsură numerică a mişcării de rotaţie se conservă? Motoarele maşinilor şi discurile LP (long play) de modă veche (plăcile de patefon) au viteza de rotaţie măsurată în rotaţii pe minut (r.p.m.), însă numărul de rotaţii pe minut (sau pe secundă) nu reprezintă o cantitate conservată. De exemplu mâna patinatoarei din imagine care execută răsucirea poate creşte numărul de rotaţii pe minut prin apropierea mâinilor de corp.
Exemplul cu patinatoarea sugerează că această cantitate conservată depinde de distanţa faţă de axul de rotaţie. Vom nota această distanţă cu r, astfel încât pentru un obiect aflat în mişcare circulară în jurul axei sale de rotaţie, distanţa faţă axă va fi egală cu raza cercului.
Din momentul în care realizăm că r este o variabilă care contează, devine clar că toate exemplele pe care le-am luat în considerare sunt destul de complicate din punct de vedere matematic, deoarece diferite părţi ale maselor acestor obiecte au diferite valori ale lui r. De exemplu, dinţii din faţă ai patinatoarei sunt mai departe de axă decât dinţii din spate. Asta sugerează că în loc de obiecte cu forme complicate va trebui să luăm în considerare cel mai simplu exemplu, cum ar fi o particulă cu masa m călătorind într-un cerc de rază r la viteza v. Experimentele arată că în această situaţie cantitatea conservată este ± mvr.
Numim această cantitate moment cinetic. Simbolul ± indică faptul că momentul cinetic are, pentru a reprezenta direcţia rotaţiei, semn pozitiv sau negativ; spre exemplu, într-o problemă dată, putem alege să reprezentăm momentele unghiulare în sensul acelor de ceasornic ca numere pozitive sau ca numere negative. În această ecuaţie singura viteză care contează este viteză care este perpendiculară pe linia razei; mişcarea paralelă cu linia razei, adică în mod direct în afara noastră, nu este nici în sensul acelor de ceasornic, nici în sens invers acelor de ceasornic.
Exemplul 1: O patinatoare îşi apropie braţele de corp

a. O patinatoare apropie braţele de corp, rotindu-se mai repede
În momentul în care patinatoarea din figura A îşi apropie braţele de corp, r scade pentru totalitatea atomilor care-i formează mâna. Asta ar încălca conservarea momentului cinetic dacă ar continua rotaţia cu aceeaşi viteză, de exemplu dacă timpului pentru fiecare rotaţie ar fi acelaşi, deoarece braţele sale vor fi mai apropiate de axa de rotaţie şi prin urmare va avea un r mai mic (dar şi un v mai mic, desigur, deoarece braţele vor completa un cerc mai mic în acelaşi timp). Acest lucru este imposibil, deoarece ar încălca legea conservării momentului cinetic. Dacă momentul cinetic total va rămâne constant, scăderea momentului cinetic pentru braţele sale va trebui compensată de o creştere a ratei de rotaţie. Adică - apropiindu-şi braţele de corp, se reduce substanţial timpul pentru fiecare rotaţie.
Exemplul 2: Un săritor în lungime

b. Fotografie veche a unui săritor în lungime
În figura b, săritorul vrea să-şi aducă picioarele în faţa lui, în aşa fel încât să nu aterizeze în cap. Propulsându-şi picioarele înainte implică o anumită rotaţiei în sensul contrar acelor de ceasornic, dar el nu a început cu vreo rotaţie atunci când s-a desprins de sol. Să considerăm mişcarea în sensul opus acelor de ceasornic ca fiind pozitivă şi mişcarea în sensul acelor de ceasornic ca fiind negativă. Singura modalitate ca picioarele sale să obţină o rotaţie pozitivă este dacă o parte a corpului său preia o cantitate egală a rotaţiei negative. Acesta este motivul pentru care îşi mişcă braţele către în spate, în sensul acelor de ceasornic.
Exemplul 3: Modificarea axei

c. Tânăr cântând la violă
Momentul cinetic al unui obiect poate fi diferit, depinzând de axa în jurul căreia se roteşte, deoarece r este definit în raport cu axa de rotaţie. Figura c prezintă două duble expuneri ale fotografiei cu un cântăreţ la violă care basculează arcuşul pentru a trece de la o coardă la alta. Un moment cinetic mai mare este necesar atunci se ating coardele cu zona din apropierea mânerului arcuşului, numită broască, la fel ca în imaginea din dreapta; nu numai că majoritatea atomilor din arc sunt la distanţe mai mari de la axa de rotaţie, dar cei din vârf au, de asemenea, o viteză v mai mare. Este dificil pentru cântăreţ să transfere repede un moment cinetic mare în arc şi apoi să-l transfere înapoi la fel de repede. Acesta este unul din motivele pentru care violoniştii experimentaţi tind să rămână aproape de mijlocul arcuşului cât de mult posibil.
Exemplul 4 : Legea lui Kepler
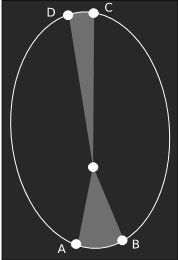
d. Orbită planetă
Planeta ipotetică din figura d are o orbită în care punctul cel mai apropiat de Soare reprezintă o distanţă aflată la jumătatea distanţei până la punctul în care planeta se află la cea mai mare distanţă faţă de stea. Întrucât momentul cinetic, mvr, este conservat, iar masa planetei este constantă, cantitatea vr trebuie să fie aceeaşi la ambele capete ale orbitei. Dublarea razei necesită o reducere la jumătatea a vitezei v. În cazul în care timpul necesar deplasării de la A la B este acelaşi ca cel necesar deplasării de la C la D, atunci distanţa de la C la D trebuie să fie la jumătate din AB. Iar asta este exact ceea ce legea suprafeţelor egale a lui Kepler afirmă, deoarece parcela structurii radiale a triunghiului de sus trebuie să aibă jumătate din lăţimea pentru a compensa înălţimea dublă. Cu alte cuvinte, legea suprafeţelor egale este o consecinţă directă a conservării momentului cinetic.
