 Cel mai mare triumf al lui Isaac Newton a fost explicaţia sa asupra mişcării planetelor aplicând legi ale fizicii universal valabile. A fost o imensă revoluţie a gândirii: pentru prima data atât Pământul, cât şi cerul au fost văzute ca funcţionând în mod automat, după aceleaşi reguli. Newton nu ar fi a fost capabil să îşi dea seama de ce planetele se mişcă în felul în care se mişcă dacă nu ar fi fost astronomul Tycho Brahe (1546-1601) şi protejatul său Johann Kepler (1571-1630), care au realizat împreună prima descriere simplă şi precisă a modului în care se mişcă planetele de fapt.
Cel mai mare triumf al lui Isaac Newton a fost explicaţia sa asupra mişcării planetelor aplicând legi ale fizicii universal valabile. A fost o imensă revoluţie a gândirii: pentru prima data atât Pământul, cât şi cerul au fost văzute ca funcţionând în mod automat, după aceleaşi reguli. Newton nu ar fi a fost capabil să îşi dea seama de ce planetele se mişcă în felul în care se mişcă dacă nu ar fi fost astronomul Tycho Brahe (1546-1601) şi protejatul său Johann Kepler (1571-1630), care au realizat împreună prima descriere simplă şi precisă a modului în care se mişcă planetele de fapt.
CUPRINS
2.4 Triumful lui Newton
Dificultatea sarcinii lor este reprezentată în figura q, care arată cum mişcările orbitale, relativ simple, ale Pământului şi planetei Marte se combină, astfel încât, văzut de pe Pământ, Marte pare a se deplasa în curbe ca un marinar beat.

r. Tycho Brahe şi-a creat un nume ca astronom arătând că o stea strălucitoare nouă, azi numită supernovă, care a apărut pe cerul lui 1572, a fost foarte departe de atmosfera Pământului. Aceasta, împreună cu descoperirea lui Galileo a petelor solare, a arătat că în opoziţie cu teoria lui Aristotel, cerurile nu sunt perfecte şi neschimbătoare. Faima lui Brahe ca astronom, i-a adus sprijinul regelui Frederik II, permiţându-i să efectueze măsurătorile sale de înaltă precizie asupra mişcării planetelor. Un caracter contradictoriu, Brahe aprecia romane scrise de alţi nobile în care se evidenţiau defectele duelului, dar şi-a pierdut nasul într-un duel în tinereţe, pe care şi l-a înlocuit cu o proteză, alcătuită dintr-un aliaj de aur cu argint. Dispus să suporte scandalul, cu scopul de a se căsători cu o ţărancă, el şi-a folosit puterile dăruite lui de către rege pentru a le impune munci dure locuitorilor de pe feuda sa. Rezultatul muncii lor: un palat în stil italian cu un observator în vârf, cu siguranţă unul dintre cele mai luxoase laboratoare științifice din lume. El a murit din cauza perforării vezici biliare după căderea dintr-o caleaşcă în drumul spre casă de la o petrecere; în acea vreme era considerat nepoliticos să părăseşti cina pentru a te “calma”.
Brahe, ultimul mare astronom care practica meseria cu ochiul liber, a colectat numeroase date despre mişcarea planetelor pe o perioadă de mai mulţi ani, făcând un pas uriaş de la precizia observaţiilor anterioare de 10 minute pe arc (10/60 dintr-un grad) la o nemaivăzută precizie de 1 minut. Rezultatul muncii sale este cu atât mai remarcabil, având în vedere că observatorul său a constat în patru raportoare de alamă gigantice, montate în poziţie verticală în castelul său din Danemarca. Patru observatori măsurau simultan poziţia unei planete cu scopul de a verifica greşelile şi de a reduce erorile.
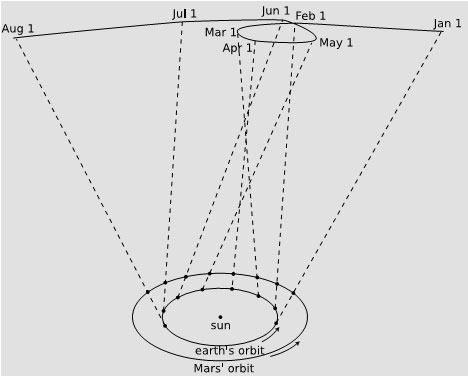
q. Deoarece Terra şi Marte se deplasează în jurul Soarelui cu viteze diferite, efectul combinat al mişcării lor face ca Marte să pară că trasează o urmă ciudată, curbată, pe fundalul stelelor îndepărtate
După moartea lui Brahe, a căzut pe seama fostului său asistent, Kepler, sarcina de a analiza acest mare volum de date. Kepler, în mod contrar maestrului său, şi-a format o intuiţie, dovedită corectă, în favoarea teoriei conform cărei Pământul şi planetele se învârt în jurul Soarelui, nu Pământul stă şi toate corpurile se învârt în jurul lui. Deşi mişcarea este relativă, întrebarea „cine înconjoară pe cine” nu este doar o chestiune de opinie. Mişcările de rotaţie şi de revoluţie ale Pământului îl fac un sistem de referinţă non-inerţial, lucru care duce la încălcări vizibile ale legilor lui Newton când cineva încearcă să descrie cu un grad de precizie rezonabil experimente în sistemul de referinţă fix al Pământului. Deşi asemenea experimente directe nu au fost efectuate până în secolul al XIX-lea, ceea ce a convins întreaga lume de valabilitatea teoriei heliocentriste în secolul al XVII-lea a fost faptul că Kepler a fost capabil să dezvolte un surprinzător set de reguli matematice şi geometrice pentru mişcarea planetelor folosind teoria heliocentristă. După 900 de pagini de calcule şi multe încercări nereuşite, în final Kepler a sintetizat în trei legi.
Citeşte şi: Legile lui Kepler pe înţelesul tuturor
1. Legea orbitelor eliptice a lui Kepler
Planetele se învârt în jurul soarelui pe orbite eliptice, cu Soarele în centru.
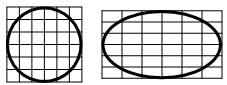
s. O elipsă este un cerc care a fost deformat prin turtirea şi alungirea de-a lungul unei axe perpendiculare
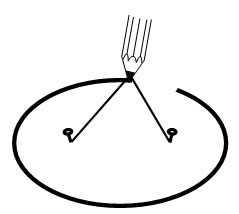
t. O elipsă poate fi construită legând o sfoară de două cuie şi desenând cu creionul, întinzând sfoara, la fel ca în desen
2. Legea ariilor egale a lui Kepler
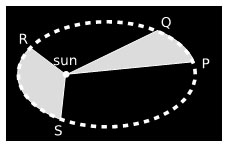
u. Dacă intervalul de timp în care planeta se mişcă de la P la Q este egal cu intervalul de la R la S, atunci conform legii ariei egale a lui Kepler, cele două zone umbrite sunt egale. Planeta se mişcă mai repede de-a lungul intervalului RS decât se mişcă de-a lungul intervalului PQ; Newton a determinat mai târziu că accelerarea ei se datorează forţei gravitaţionale a Soarelui. Legea egalităţii ariei prevede exact cât de mult va accelera.
Linia care uneşte planeta cu Soarele “desenează” arii egale în intervale egale de timp.
3. Legea perioadelor a lui Kepler
Să notăm cu T perioada în care planeta înconjoară Soarele şi să notăm cu a axa lungă a elipsei. T2 este proporţional cu a3.
Deşi orbitele planetelor sunt mai mult elipse decât cercuri, multora le mai lipseşte puţin să devină cercuri. Orbita Pământului, de exemplu, este turtită cu 1,7% în comparaţie cu un cerc. În cazul special al unei planete cu o orbită circulară, cele două centre corespund cu centrul cercului, iar legea orbitei eliptice a lui Kepler spune că centrul este plasat pe Soare. Legea ariei egale menţionează că o planetă aflată pe o orbită circulară se mişcă în jurul Soarelui cu viteză constantă. Pentru o orbită circulară, legea perioadelor se rezumă la afirmaţia că T2 este proporţional cu r3, unde r este raza. Dacă toate planetele se deplasează pe orbitele lor cu aceeaşi viteză, atunci timpul necesar efectuării unei orbite creşte doar odată cu circumferinţa cercului, deci există o proporţionalitate simplă între T şi r. Întrucât nu este cazul, putem interpreta legea perioadelor ca însemnând că diferite planete orbitează în jurul Soarelui la viteze diferite. De fapt planetele exterioare se mişcă mai încet decât planetele interioare.
Exemplul 13. Jupiter şi Uranus
Planetele Jupiter şi Uranus au orbite aproape circulare, iar raza orbitei lui Uranus este de 4 ori mai mare decât cea a orbitei lui Jupiter. Comparaţi-le perioadele orbitale.
Dacă toate planetele se mişcă la aceeaşi viteză, atunci lui Uranus îi va lua de patru ori mai mult timp pentru a străbate orbita sa, cu o circumferinţă de patru ori mai mare. Oricum , legea perioadelor ne spune că nu este cazul. Ne aşteptăm ca lui Uranus să îi i-a mai mult decât de patru ori străbaterea orbitei sale.
Legea perioadelor este reprezentată ca o proporţionalitate, iar proporţionalităţile sunt afirmaţii despre mărimi în raport cu alte mărimi. Ştim cât este raza orbitei lui Uranus, împărţită la cea a lui Jupiter. Să denumim această proporţie y. Apoi căutăm un număr y pentru care:
Y2 = 43
y x y = 4 x 4 x 4
y x y = 64
y = 8
Legea perioadelor prezice faptul că perioada lui Uranus va fi de opt ori mai mare decât a lui Jupiter, lucru care este observat cu adevărat (lipsa preciziei este de aşteptat având în vedere că cifra 4 a fost aproximată ca număr întreg, pentru uşurinţă în calcul).
Ce a descoperit Newton este motivul pentru care legile lui Kepler sunt adevărate: el a arătat că ele rezultă din legile sale ale mişcării. Dintr-un punct de vedere modern, legile conservării sunt mai “fundamentale” decât legile lui Newton, astfel că decât să urmărim abordarea lui Newton, are mai mult sens să căutăm motivele pentru care legile lui Kepler rezultă din legile conservării. Legea suprafeţelor egale este mai uşor de înţeles ca o consecinţă a conservării impulsului unghiular, care este o nouă mărime conservată despre care vom discuta în capitolul 3. Dovada legii orbitei eliptice este un pic prea matematică pentru a fi abordată în această carte.

v. Conectând legea perioadelor a lui Kepler cu legile fizici
Legea perioadelor derivă direct din fizica pe care deja am discutat-o. Să luăm exemplul lui Jupiter şi a lui Uranus. Vrem să arătăm că rezultatul din exemplul 13 este singurul în concordanţă cu legile de conservarea energiei şi a impulsului şi cu legea gravitaţiei a lui Newton. Deoarece lui Uranus îi ia de opt ori mai mult timp pentru a acoperi o distanţă de patru ori mai mare, se mişcă, evident, cu jumătate din viteza lui Jupiter. În figura v distanţa străbătută de Jupiter de la A la B este prin urmare de două ori distanţa străbătută în acelaşi timp de Uranus de la D la E. Dacă nu ar exista nicio forţă gravitaţională exercitată de Soare, Jupiter ar ajunge la C, iar Uranus la F. Distanţa de la B la C este un indicator al forţei cu care se acţionează asupra lui Jupiter; la fel şi pentru distanţa foarte mică de la E la F. BC are 16 milimetri la scara desenului, iar EF are 1 milimetru, dar este exact ceea ce ne aşteptam de la legea gravitaţiei a lui Newton: înmulţind cu 4 distanţa ar trebui să obţinem o forţă de 1/16.
