
Algoritmii sunt o parte esenţială din instrumentarul oricărui programator, dar cunoştinţe de bază despre subiect pot fi de ajutor şi neprogramatorilor în rezolvarea de probleme. În articolul de faţă vom vorbi despre o metodă de rezolvare a problemelor numită Divide et impera şi vom explica un algoritm de sortat numere folosind această metodă.
Să luăm o listă de numere aleatorii. Un algoritm simplu ar fi să comparăm fiecare număr cu fiecare număr și să aflăm ordinea numerelor. În acest caz, ne vom lovi de o problemă, numărul de operații va fi o funcție de n2, unde n este numărul de elemente din listă. Asta înseamnă că dacă vom mări numărul de elemente, numărul de operații necesare va crește exponențial, crescând din ce în ce mai mult timpul în care informația este procesată de calculator.
În acest caz, vom apela la metoda denumită Divide et impera. Divide et impera constă în descompunerea problemei date în mai multe subprobleme ce pot fi rezolvate mai ușor. Pe lângă Divide et impera, ne vom folosi și de recursivitate.
În loc de a lucra cu lista întreagă de numere, vom împărți lista în două liste mai mici, iar pe cele două din nou în câte 2 alte liste șamd. până ajungem la un caz de bază (o listă cu un singur element, în această situație). Vom folosi un "copac de recursivitate" pentru a ilustra această idee:
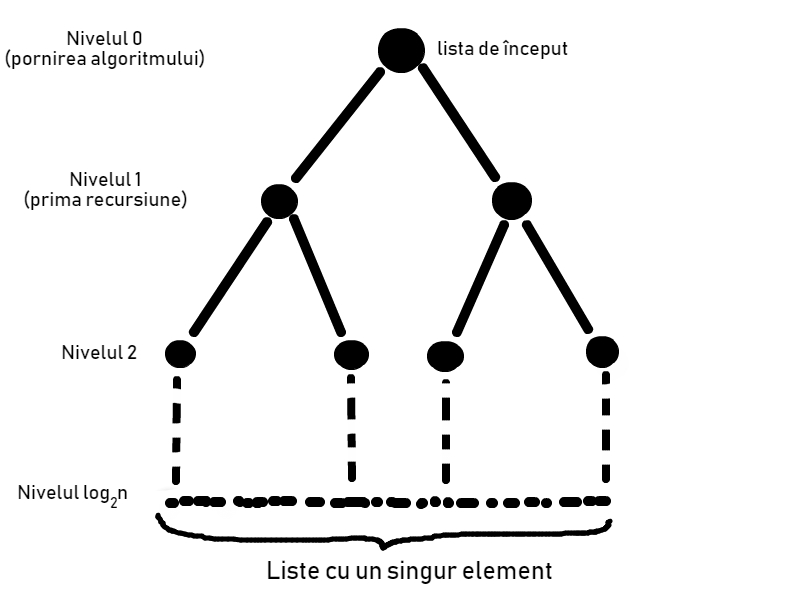
După cum putem observa, la fiecare nivel din diagramă numărul de liste formate va fi 2j, unde j este numărul nivelului, iar lungimea fiecărei liste va fi n/2j.
Odată ce ajungem la cazul de bază, algoritmul va lua cele 2 liste de un element de pe acea ramură a copacului și va compara numărul din prima listă cu cel din a doua listă și le va sorta crescător. După aceea, lista sortată este comparată din nou cu încă o listă sortată de pe o ramură alăturată, recursiv, până ajungem la o singură listă cu toate numerele de la început sortate. Acesta este pseudo-codul algoritmului:
| A = prima listă [lungimea n/2] B = a doua listă [lungimea n/2] C = lista sortată [lungimea n] l = 1 m = 1 pentru k = 1 până la n -> o operație dacă l < n/2 -> o operație dacă m < n/2 dacă A[l] < B[m] -> o operație C[k] = A[l] -> o operație l++ -> o operație altfel dacă B[m] < A[l] C[k] = B[m] m++ altfel C[k] = A[l] l++ altfel C[k] = B[m] -> o operație m++ -> o operație final |
După cum puteți vedea, această parte a algoritmului are aproximativ 6n operații unde n este numărul de elemente total din listele procesate. Dacă aceste operații sunt repetate pentru fiecare listă de la un nivel anume, atunci numărul de operații totale la un nivel j va fi maxim numărul de liste la acel nivel înmulțit cu numărul de operații necesare pentru fiecare listă, adică:
2j * 6(n/2j) = 6n
Dacă la orice nivel j, numărul de operații necesare este 6n, atunci, în total, tot algoritmul va avea nevoie de cel mult numărul de operații la orice nivel înmulțit cu numărul de niveluri în total, deci:
6n(log2n + 1) = 6n * log2n + 6n
Deci, am reușit să creăm un algoritm de sortare care are un număr necesar de operații o funcție de n * log2n, o funcție mult mai eficientă decât cea de n2 prezentată la începutul articolului.
Iată mai jos codul scris de mine, în C++, pentru realizarea sortării explicate mai sus. Am păstrat comentariile în limba engleză, aşa cum le-am scris iniţial.
| #include "stdafx.h" #include <iostream> #include <vector> using namespace std; // function to merge 2 sublists into 1 sorted sublist vector<int> Merge(vector<int>& split_lo, vector<int>& split_hi) { // setup output variable -> merged, sorted list of the 2 input sublists vector<int> out; int l = 0; int m = 0; // loop through all the elements of the 2 sublists for (size_t k = 0; k < split_lo.size() + split_hi.size(); k++) { // check if we reached the end of the first sublist if (l < split_lo.size()) { // check if we reached the end of the second sublist if (m < split_hi.size()) { // check which element is smaller and sort accordingly if (split_lo[l] < split_hi[m]) { out.push_back(split_lo[l]); l++; } else if (split_hi[m] < split_lo[l]) { out.push_back(split_hi[m]); m++; } } else { out.push_back(split_lo[l]); l++; } } else { out.push_back(split_hi[m]); m++; } } return out; } // function that loops itself recursively to split input into halves until it reaches the base case (1 element array) vector<int> MergeSort_and_CountInversions(vector<int>& V) { // if we reached the base case, terminate the loop and feed the output to the previous loop to be processed if (V.size() == 1) return V; // if we didn't reach the base case else { // continue halving the sublists size_t const half_size = V.size() / 2; vector<int> split_lo(V.begin(), V.begin() + half_size); vector<int> split_hi(V.begin() + half_size, V.end()); // feed them back into the loop return Merge_and_Count(MergeSort_and_CountInversions(split_lo), MergeSort_and_CountInversions(split_hi)); } } // main function of the app, runs everything int main() { // setup main variables int input; vector<int> V; // get input cout << "Enter your numbers to be sorted (enter Y when you wish to proceed to the sorting)." << endl; cout << "Note: do NOT use duplicates (for example, do not input 1 and 1 again)!" << endl; while (cin >> input) V.push_back(input); cout << "\nThe numbers you chose were: " << endl; for (size_t i = 0; i < V.size(); i++) cout << V[i] << " "; // get sorted output vector<int> sorted = MergeSort_and_CountInversions(V); cout << "\n\nHere are your numbers sorted: " << endl; for (size_t j = 0; j < sorted.size(); j++) cout << sorted[j] << " "; return 0; } |

